题目内容
7.数列{an}的前n项的和为Sn,求证:“Sn=an2+bn,a,b∈R”是“数列{an}为等差数列”的充要条件.分析 由等差数列的求和公式和通项公式,分别证明必要性和充分性即可.
解答 证:充分性:当n=1时,a1=a+b;当n≥2时,an=Sn-Sn-1=2an+b-a,
显然当n=1时也满足上式,
∴an-an-1=2a
∴{an}是等差数列.
必要性:∵数列{an}为等差数列,
∴Sn=na1+$\frac{n(n-1)}{2}$d=$\frac{d}{2}$n2+(a1-$\frac{d}{2}$)n,
令a=$\frac{d}{2}$,b=a1-$\frac{d}{2}$,则Sn=an2+bn,a,b∈R.
综上,“Sn=an2+bn,a,b∈R”是“数列{an}为等差数列”的充要条件.
点评 本题考查充要条件的证明,考查等差数列的定义与求和,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
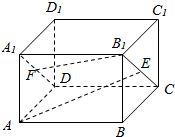 如图,在长方体ABCD-A1B1C1D1中,E是矩形BCC1B1的中点,F是矩形ADD1A1的中心,连接AE,B1F,判断AE与B1F是否为异面直线.
如图,在长方体ABCD-A1B1C1D1中,E是矩形BCC1B1的中点,F是矩形ADD1A1的中心,连接AE,B1F,判断AE与B1F是否为异面直线.