题目内容
已知双曲线的中心在原点,右顶点为A(1,0)点P、Q在双曲线的右支上,支M(m,0)到直线AP的距离为1(Ⅰ)若直线AP的斜率为k,且
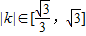 ,求实数m的取值范围;
,求实数m的取值范围;(Ⅱ)当
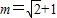 时,△APQ的内心恰好是点M,求此双曲线的方程.
时,△APQ的内心恰好是点M,求此双曲线的方程.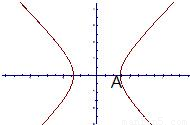
【答案】分析:(Ⅰ)设出直线AB的方程,表示出点M到直线AP的距离求得m-1的范围.
(Ⅱ)设双曲线方程,由M和A求得|AM|,又因为M是△APQ的内心,M到AP的距离为1,所以∠MAP=45°,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1,求得P点坐标,代入椭圆方程求得b,求得双曲线方程.
解答:解:(Ⅰ)由条件得直线AP的方程y=k(x-1),
即kx-y-k=0.
因为点M到直线AP的距离为1,
∵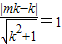 ,
,
即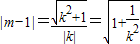 .
.
∵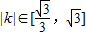 ,
,
∴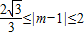 ,
,
解得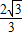 +1≤m≤3或--1≤m≤1--
+1≤m≤3或--1≤m≤1--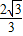 .
.
∴m的取值范围是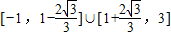 .
.
(Ⅱ)可设双曲线方程为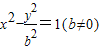 ,
,
由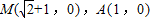 ,
,
得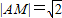 .
.
又因为M是△APQ的内心,M到AP的距离为1,所以∠MAP=45°,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1 因此,kAP=1,kAQ=-1(不妨设P在第一象限)
因此,kAP=1,kAQ=-1(不妨设P在第一象限)
直线PQ方程为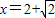
直线AP的方程y=x-1,
∴解得P的坐标是(2+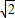 ,1+
,1+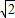 ),将P点坐标代入
),将P点坐标代入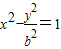 得,
得,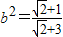
所以所求双曲线方程为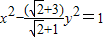 ,
,
即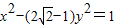 .
.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合运用所学知识解决问题的能力.
(Ⅱ)设双曲线方程,由M和A求得|AM|,又因为M是△APQ的内心,M到AP的距离为1,所以∠MAP=45°,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1,求得P点坐标,代入椭圆方程求得b,求得双曲线方程.
解答:解:(Ⅰ)由条件得直线AP的方程y=k(x-1),
即kx-y-k=0.
因为点M到直线AP的距离为1,
∵
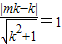 ,
,即
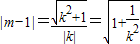 .
.∵
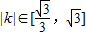 ,
,∴
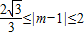 ,
,解得
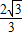 +1≤m≤3或--1≤m≤1--
+1≤m≤3或--1≤m≤1--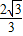 .
.∴m的取值范围是
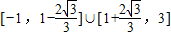 .
.(Ⅱ)可设双曲线方程为
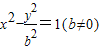 ,
,由
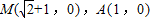 ,
,得
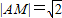 .
.又因为M是△APQ的内心,M到AP的距离为1,所以∠MAP=45°,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1
 因此,kAP=1,kAQ=-1(不妨设P在第一象限)
因此,kAP=1,kAQ=-1(不妨设P在第一象限)直线PQ方程为
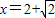
直线AP的方程y=x-1,
∴解得P的坐标是(2+
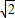 ,1+
,1+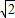 ),将P点坐标代入
),将P点坐标代入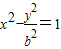 得,
得,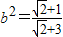
所以所求双曲线方程为
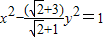 ,
,即
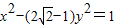 .
.点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合运用所学知识解决问题的能力.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目