题目内容
已知两条直线l1:x+(1+m)y+m-2=0,l2:mx+2y+8=0,当m为何值时直线l1与l2分别有下列关系?
(1)l1⊥l2;
(2)l1∥l2.
(1)l1⊥l2;
(2)l1∥l2.
分析:(1)利用两直线垂直的充要条是 A1A2+B1B2=0,可得 1×m+(1+m)•2=0,由此求得解得m的值.
(2)由两直线平行的充要条件是
=
≠
,可得
=
≠
,由此求得解得m的值.
(2)由两直线平行的充要条件是
| A1 |
| A2 |
| B1 |
| B2 |
| C1 |
| C2 |
| A1 |
| A2 |
| B1 |
| B2 |
| C1 |
| C2 |
解答:解:(1)∵两条直线l1:x+(1+m)y+m-2=0,l2:mx+2y+8=0,由两直线垂直的充要条件可得 A1A2+B1B2=0,
即 1×m+(1+m)•2=0,解得m=-
.
(2)由两直线平行的充要条件可得
=
≠
,即
=
≠
,
解得 m=1.
即 1×m+(1+m)•2=0,解得m=-
| 2 |
| 3 |
(2)由两直线平行的充要条件可得
| A1 |
| A2 |
| B1 |
| B2 |
| C1 |
| C2 |
| 1 |
| m |
| 1+m |
| 2 |
| m-2 |
| 8 |
解得 m=1.
点评:本题主要考查两直线平行的性质,两直线垂直的性质,利用了两直线垂直的充要条是 A1A2+B1B2=0,两直线平行的充要条件是
=
≠
,属于基础题.
| A1 |
| A2 |
| B1 |
| B2 |
| C1 |
| C2 |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
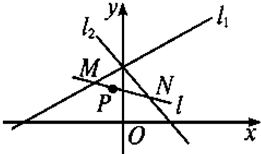 如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.
如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.