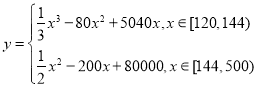题目内容
【题目】如图,在平面直角坐标系xOy中,已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且右焦点到右准线l的距离为1.过x轴上一点M(m,0)(m为常数,且m∈(0,2))的直线与椭圆C交于A,B两点,与l交于点P,D是弦AB的中点,直线OD与l交于点Q.
,且右焦点到右准线l的距离为1.过x轴上一点M(m,0)(m为常数,且m∈(0,2))的直线与椭圆C交于A,B两点,与l交于点P,D是弦AB的中点,直线OD与l交于点Q.

(1) 求椭圆C的标准方程.
(2) 试判断以PQ为直径的圆是否经过定点.若是,求出定点坐标;若不是,请说明理由.
【答案】(1)![]() +y2=1;(2)是,定点
+y2=1;(2)是,定点![]()
【解析】
(1)由已知列出![]() 方程组解得
方程组解得![]() ,然后求得
,然后求得![]() ,得椭圆标准方程;
,得椭圆标准方程;
(2)首先确定直线AB斜率存在且不为0,然后设直线方程为y=k(x-m),求出P,Q点,写出圆的方程(直径式),然后,即令斜率k的系数为零,常数项也为零,得出关于x,y的方程可得定点.审题注意题中m是常数,而非变量.
(1)由题意,得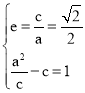 ,解得
,解得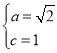 所以a2=2,b2=1,
所以a2=2,b2=1,
所以椭圆C的标准方程为![]() +y2=1.
+y2=1.
(2) 由题意,当直线AB的斜率不存在或为零时显然不符合题意,所以可设直线AB的斜率为k,则直线AB的方程为y=k(x-m).
又准线方程为x=2,
所以点P的坐标为P(2,k(2-m)).
由![]() 得,x2+2k2(x-m)2=2,即(1+2k2)x2-4k2mx+2k2m2-2=0,
得,x2+2k2(x-m)2=2,即(1+2k2)x2-4k2mx+2k2m2-2=0,
所以xA+xB=![]() ,则xD=
,则xD=![]() ·
·![]() =
=![]() ,yD=k
,yD=k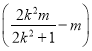 =-
=-![]() ,
,
所以kOD=-![]() ,
,
从而直线OD的方程为y=-![]() x(也可用点差法求解),
x(也可用点差法求解),
所以点Q的坐标为Q![]() .
.
所以以P,Q为直径的圆的方程为(x-2)2+![]() (y-k(2-m))=0,
(y-k(2-m))=0,
即x2-4x+2+m+y2-[ k(2-m)-![]() ]y=0.
]y=0.
因为该式对k≠0恒成立,令y=0,得x=2±![]() ,
,
所以,以PQ为直径的圆经过定点![]() .
.

【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(1)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(2)在上述样本中,学校从成绩为![]() 的学生中随机抽取
的学生中随机抽取![]() 人进行学习交流,求这
人进行学习交流,求这![]() 人来自同一个班级的概率.
人来自同一个班级的概率.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|