题目内容
已知函数(2)若函数f(x)的图象按向量
解析: (1)f(x)=asin2x+bcos2x =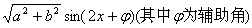
由已知条件得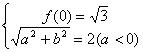
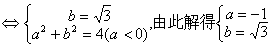
∴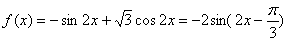
于是由f(x)单调递增得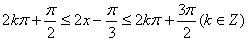
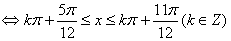
∴所求f(x)的递增区间为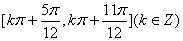 .
.
(2)注意到 故函数y=f(x)图象按向量
故函数y=f(x)图象按向量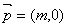 平移后的图象对应的函数解析式为
平移后的图象对应的函数解析式为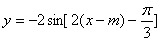 即
即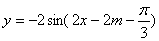 ①
①
注意到函数①的图象关于y轴对称 ∴函数①为偶函数
∴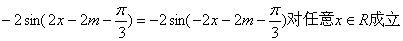
∴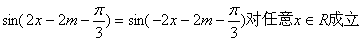 . ②
. ②
在②中令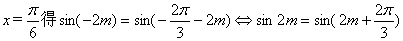
由此得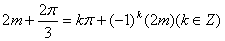 ③ 注意到当k为偶数时③无解,故由③得
③ 注意到当k为偶数时③无解,故由③得
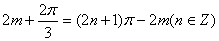 ∴
∴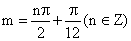 ∴m的绝对值最小的取值为
∴m的绝对值最小的取值为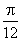
此时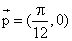 且由①得
且由①得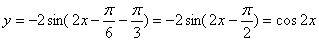
因此,所求向量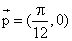 ,平移后的图象对应的函数解析式为y=cos2x.
,平移后的图象对应的函数解析式为y=cos2x.
由已知条件得
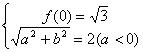
∴
于是由f(x)单调递增得
∴所求f(x)的递增区间为
(2)注意到
注意到函数①的图象关于y轴对称 ∴函数①为偶函数
∴
∴
在②中令
由此得
此时
因此,所求向量

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象过点A(3,7),则此函的最小值是 .
的图象过点A(3,7),则此函的最小值是 . 的图象过点
的图象过点 ,且图象上与点P最近的一个最低点是
,且图象上与点P最近的一个最低点是 .
. 的解析式;
的解析式; ,且
,且 为第三象限的角,求
为第三象限的角,求 的值;
的值; 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围. 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数