题目内容
已知等差数列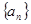 的公差大于0,且
的公差大于0,且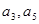 是方程
是方程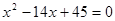 的两根,数列
的两根,数列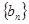 的前n项的和为
的前n项的和为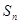 ,且
,且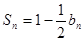 .
.
(1)求数列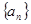 ,
,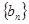 的通项公式;
的通项公式;
(2)记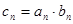 ,求证:
,求证: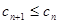 .
.
(1)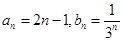 ; (2)详见解析.
; (2)详见解析.
解析试题分析:(1) 求等差数列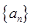 的通项公式,只需求出
的通项公式,只需求出 即可,因为
即可,因为 是方程
是方程 的两根,且数列
的两根,且数列 的公差
的公差 , 这样可求出
, 这样可求出 ,从而可得数列
,从而可得数列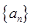 的通项公式,又因为数列
的通项公式,又因为数列 的前
的前 项和为
项和为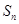 ,
, ,可利用
,可利用 得到递推关系,
得到递推关系, ,得出
,得出  ,数列
,数列 是等比数列,根据等比数列的通项公式写出
是等比数列,根据等比数列的通项公式写出 ; (2) 记
; (2) 记 ,求证:
,求证: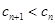 ,首先写出数列
,首先写出数列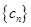 的通项公式,
的通项公式, , 要证明
, 要证明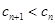 ,可用作差比较法,只需证
,可用作差比较法,只需证 即可.
即可.
试题解析:(1)∵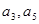 是方程
是方程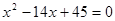 的两根,且数列
的两根,且数列 的公差d>0,
的公差d>0,
∴ ,公差
,公差
∴ 3分
3分
又当 时,有
时,有 ,-所以
,-所以 ,
,
当
∴数列 是等比数列,
是等比数列,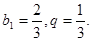
∴ 6分
6分
(2)由(1)知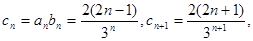 9分
9分
∴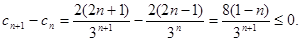
∴ 12分
12分
考点:数列与不等式的综合,等差数列的通项公式,等比数列的通项公式,等比数列的通项公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
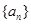 ,其前
,其前 项和
项和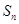 满足
满足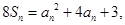 且
且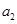 是
是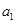 和
和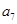 的等比中项..
的等比中项..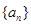 的通项公式;
的通项公式;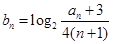 ,求数列
,求数列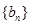 的前99项和.
的前99项和.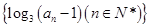 为等差数列,且
为等差数列,且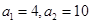 .
.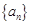 的通项公式;
的通项公式;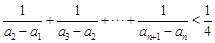 .
.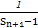 ,其前n项和为Tn,求证:Tn<
,其前n项和为Tn,求证:Tn< (n∈N*).
(n∈N*).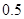 万人,从2023年开始到2032年每年人口为上一年的99%.
万人,从2023年开始到2032年每年人口为上一年的99%. 年的人口总数
年的人口总数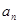 的表达式(注:2013年为第一年);
的表达式(注:2013年为第一年);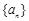 的前
的前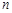 项和为
项和为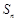 ,已知
,已知 ,
,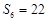 .
.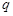 的等比数列
的等比数列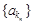 ,其中
,其中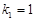 ,且
,且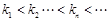 ,
,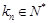 .
.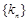 的通项公式;
的通项公式; 的不等式
的不等式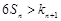 有解,试求
有解,试求