题目内容
（本小题满分12分）
已知椭圆M的中心为坐标原点，且焦点在x轴上，若M的一个顶点恰好是抛物线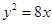
的焦点，M的离心率
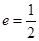，过M的右焦点F作不与坐标轴垂直的直线
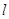，交M于A，B两点.
（1）求椭圆M的标准方程；
（2）设点N（t，0）是一个动点，且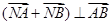
，求实数t的取值范围.
【答案】
（1）
；
（2）
【解析】(1)由抛物线焦点可得椭圆焦点F（2，0），所以可得c=2,再由离心率
,得a=1,所以椭圆方程为.
(2) 设
，
，设
(*)
下面解题的关键是把条件
直线方程和(*)式韦达定理可确定t的值.
（Ⅰ）椭圆
的标准方程：
（4分）
（Ⅱ）设，，设
由韦达定理得
①
（6分）
将
，
代入上式整理得：
，由
知
，将①代入得
（10分）
所以实数
（12分）
练习册系列答案
阅读快车系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
