题目内容
函数y=Asin(ωx+?)(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值-3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间;
(3)是否存在实数m,满足不等式Asin(ω
+φ)>Asin(ω
+φ)?若存在,求出m值(或范围),若不存在,请说明理由.
(1)求此函数解析式;
(2)写出该函数的单调递增区间;
(3)是否存在实数m,满足不等式Asin(ω
| -m2+2m+3 |
| -m2+4 |
分析:(1)根据题意,函数的最值可以确定A,根据在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值-3,可以确定函数的周期,从而求出ω的值和φ的值,从而求得函数的解析式;
(2)令 2kπ-
≤
x+
≤2kπ+
,解此不等式,即可求得函数的单调递增区间;
(3)根据(1)所求得的ω和φ的值,分析ω
+φ和ω
+φ的范围,确定函数在该区间上的单调性,即可求得结果.
(2)令 2kπ-
| π |
| 2 |
| 1 |
| 5 |
| 3π |
| 10 |
| π |
| 2 |
(3)根据(1)所求得的ω和φ的值,分析ω
| -m2+2m+3 |
| -m2+4 |
解答:解:(1)∵当x=π时,y有最大值3,当x=6π时,y有最小值-3.
∴A=
[3-(-3)]=3,
=5π,
∴T=10π=
,
∴ω=
=
,
∵当x=π时,y有最大值3,
∴
π+?=
,
∴?=
,
∴y=3sin(
x+
),
(2)令 2kπ-
≤
x+
≤2kπ+
得10kπ-4π≤x≤10kπ+π,k∈Z
∴函数的单调递增区间为:{x|10kπ-4π≤x≤10kπ+π k∈Z};
(3)∵ω=
,?=
,
∴ω
+?=
+
∈(0,
),
ω
+?=
+
∈(0,
),
而y=sint在(0,
)上是增函数
∴
+
>
+
,
∴
>
∴
,
∴
解得:
<m≤2.
∴m的取值范围是
<m≤2.
∴A=
| 1 |
| 2 |
| T |
| 2 |
∴T=10π=
| 2π |
| ω |
∴ω=
| 2π |
| 10π |
| 1 |
| 5 |
∵当x=π时,y有最大值3,
∴
| 1 |
| 5 |
| π |
| 2 |
∴?=
| 3π |
| 10 |
∴y=3sin(
| 1 |
| 5 |
| 3π |
| 10 |
(2)令 2kπ-
| π |
| 2 |
| 1 |
| 5 |
| 3π |
| 10 |
| π |
| 2 |
∴函数的单调递增区间为:{x|10kπ-4π≤x≤10kπ+π k∈Z};
(3)∵ω=
| 1 |
| 5 |
| 3π |
| 10 |
∴ω
| -m2+2m+3 |
| 1 |
| 5 |
| -(m-1)2+4 |
| 3π |
| 10 |
| π |
| 2 |
ω
| -m2+4 |
| 1 |
| 5 |
| -m2+4 |
| 3π |
| 10 |
| π |
| 2 |
而y=sint在(0,
| π |
| 2 |
∴
| 1 |
| 5 |
| -m2+2m+3 |
| 3π |
| 10 |
| 1 |
| 5 |
| -m2+4 |
| 3π |
| 10 |
∴
| -m2+2m+3 |
| -m2+4 |
∴
|
∴
|
| 1 |
| 2 |
∴m的取值范围是
| 1 |
| 2 |
点评:本题考查根据y=Asin(ωx+φ)的图象求函数的解析式以及求函数的单调区间,问题(3)的设置,增加了题目的难度和新意,易错点在于对ω
+φ∈(0,
),ω
+φ∈(0,
)的分析与应用,考查灵活应用知识分析解决问题的能力和运算能力,体现了转化的数学思想方法,属于难题.
| -m2+2m+3 |
| π |
| 2 |
| -m2+4 |
| π |
| 2 |

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
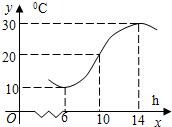 如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为
如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为
 如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若
如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若