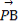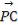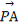题目内容
已知复数z=x+yi(x,y∈R)在复平面上对应的点为M.
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中随机取一个数作为y,求复数z为纯虚数的概率.
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组: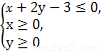 所表示的平面区域内的概率.
所表示的平面区域内的概率.
(1) 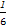 (2)
(2) 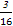
【解析】(1)记“复数z为纯虚数”为事件A.
∵组成复数z的所有情况共有12个:-4,-4+i,-4+2i,-3,-3+i,-3+2i,-2,
-2+i,-2+2i,0,i,2i,且每种情况出现的可能性相等,属于古典概型,其中事件A包含的基本事件共2个:i,2i,∴所求事件的概率为P(A)=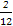 =
=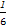 .
.
(2)依条件可知,点M均匀地分布在平面区域
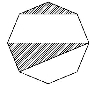
{(x,y)|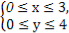 }内,属于几何概型,该平面区域的图形为图中矩形OABC围成的区域,面积为S=3×4=12.
}内,属于几何概型,该平面区域的图形为图中矩形OABC围成的区域,面积为S=3×4=12.
而所求事件构成的平面区域为
{(x,y)|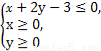 },
},
其图形为如图中的三角形OAD(阴影部分).
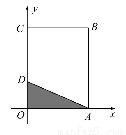
又直线x+2y-3=0与x轴、y轴的交点分别为A(3,0),D(0,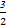 ),
),
∴三角形OAD的面积为S1=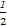 ×3×
×3×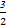 =
=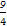 ,
,
∴所求事件的概率为P=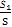 =
=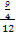 =
=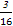 .
.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组,得到如下频率分布表:
分 组 | 频 数 | 频 率 |
[-3,-2) |
| 0.10 |
[-2,-1) | 8 |
|
(1,2] |
| 0.50 |
(2,3] | 10 |
|
(3,4] |
|
|
合计 | 50 | 1.00 |
(1)将上面表格中缺少的数据填充完整.
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率.
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.