题目内容
(理) 设函数![]() 其中
其中![]() 。(1)求
。(1)求![]() 的单调区间;
的单调区间;
(2)当![]() 时,证明不等式:
时,证明不等式:![]()
![]()
![]()
![]() ;
;
(3)设![]() 的最小值为
的最小值为![]() 证明不等式:
证明不等式:![]() 。
。
(1)单调减区间是![]() ,单调增区间是
,单调增区间是![]() 。(2)略(3)略
。(2)略(3)略
解析:
:(Ⅰ)由已知得函数![]() 的定义域为
的定义域为![]() 且
且![]()
![]()
令![]() ,解得
,解得![]() 。当x变化时,
。当x变化时,![]() 、
、![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
| 0 | + |
|
|
| 极小值 |
|
由上表可知,当![]() 时,
时,![]() 函数
函数![]() 在
在![]() 内单调递减,
内单调递减,
当![]() 时,
时,![]() 函数
函数![]() 在
在![]() 内单调递增,
内单调递增,
所以,函数![]() 的单调减区间是
的单调减区间是![]() ,函数
,函数![]() 的单调增区间是
的单调增区间是![]() 。
。
(Ⅱ)设![]() ,对
,对![]() 求导,得
求导,得![]()
![]() 。
。
当![]() 时,
时,![]()
![]() ,所以
,所以![]() 在
在![]() 内是增函数,所以
内是增函数,所以![]() 在
在![]() 上是增函数。
上是增函数。
所以当![]() 时,
时,![]() 即
即![]()
![]()
![]()
同理可证![]() 。
。
(Ⅲ)由(Ⅰ)知,![]() 将
将![]() 代入
代入![]() ,得
,得![]() ,即,
,即,![]() ,∴
,∴ ![]() 即
即![]()

练习册系列答案
相关题目
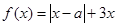 ,其中
,其中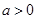 。
。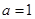 时,求不等式
时,求不等式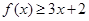 的解集;
的解集;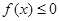 的解集为
的解集为 ,求a的值。
,求a的值。