题目内容
(12分)(理)设函数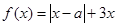 ,其中
,其中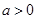 。
。
(Ⅰ)当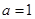 时,求不等式
时,求不等式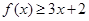 的解集;
的解集;
(Ⅱ)若不等式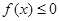 的解集为
的解集为 ,求a的值。
,求a的值。
【答案】
(Ⅰ)当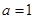 时,
时,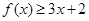 可化为
可化为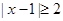 。
。
由此可得 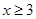 或
或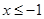 。
。
故不等式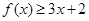 的解集为
的解集为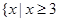 或
或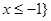 。
。
( Ⅱ) 由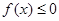 得:
得:
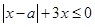
此不等式化为不等式组: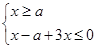 或
或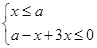 。
。
即 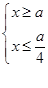 或
或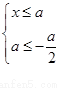
因为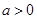 ,所以不等式组的解集为
,所以不等式组的解集为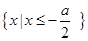 ,由题设可得
,由题设可得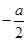 =
= 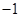 ,故
,故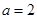 。
。
【解析】略

练习册系列答案
相关题目