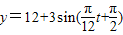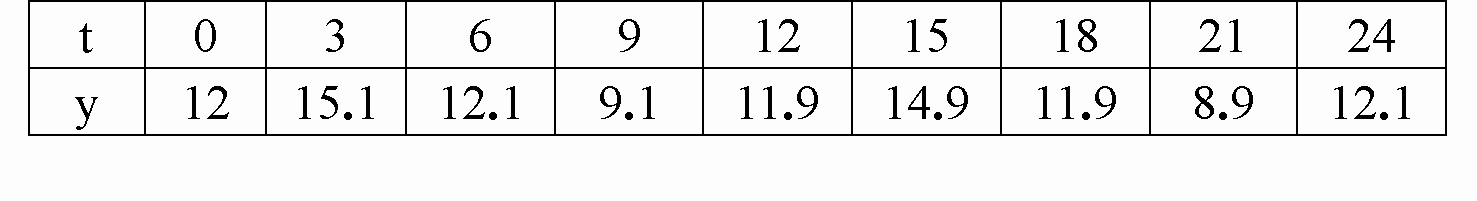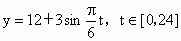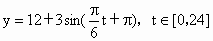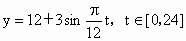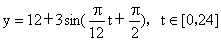题目内容
观察下面函数y=f(x)的图象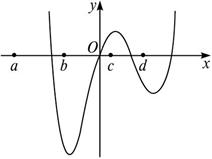
在区间[a,b]上______(有/无)零点;f(a)·f(b) ______0(<或>).
在区间[b,c]上______(有/无)零点;f(b)·f(c) ______0(<或>)
在区间[c,d]上______(有/无)零点;f(c)·f(d) ______0(<或>).
解析:根据“如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)g[f(b)]<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根”
答案:有 < 有 < 有 <

练习册系列答案
相关题目
设y=f(x)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
设y=f(x)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象,下面的函数中,最能近似表示表中数据间对应关系的函数是(t∈[0,24])( )
|
| A. |
| B. |
|
|
| C. |
| D. |
|
设y=f(x)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象,下面的函数中,最能近似表示表中数据间对应关系的函数是(t∈[0,24])( )
A.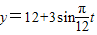
B.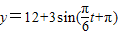
C.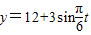
D.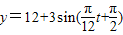
| t | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
A.
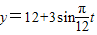
B.
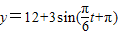
C.
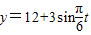
D.