题目内容
 如图,设A、B两点在河的两岸,一测量者在A的同侧所在的河岸边选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,就可以计算出A、B两点的距离为( )
如图,设A、B两点在河的两岸,一测量者在A的同侧所在的河岸边选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,就可以计算出A、B两点的距离为( )分析:由∠ACB与∠BAC,求出∠ABC的度数,根据sin∠ACB,sin∠ABC,以及AC的长,利用正弦定理即可求出AB的长.
解答:解:在△ABC中,AC=50m,∠ACB=45°,∠CAB=105°,
即∠ABC=30°,
则由正弦定理
=
,
得:AB=
=
=50
m.
故选C
即∠ABC=30°,
则由正弦定理
| AB |
| sin∠ACB |
| AC |
| sin∠ABC |
得:AB=
| ACsin∠ACB |
| sin∠ABC |
50×
| ||||
|
| 2 |
故选C
点评:此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
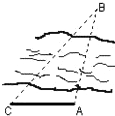 如图,设A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,就可以计算出A、B两点的距离为( )
如图,设A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,就可以计算出A、B两点的距离为( )A、50
| ||||
B、50
| ||||
C、25
| ||||
D、
|
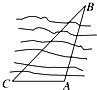 如图,设A,B两点在河的两岸,一测量者在A的同侧,在A所在的河岸边选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,则A,B两点的距离为
如图,设A,B两点在河的两岸,一测量者在A的同侧,在A所在的河岸边选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,则A,B两点的距离为 如图,设A,B两点在河的两岸,一测量者在A的同测,在所在的河岸边 选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,就可以计 算出A,B两点的距离为(精确到0.1)( )
如图,设A,B两点在河的两岸,一测量者在A的同测,在所在的河岸边 选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,就可以计 算出A,B两点的距离为(精确到0.1)( )
 m B.50
m B.50 m
m  m
m