题目内容
由曲线y=1，y=4，y=x2所围成的平面图形的面积为分析：根据对称性得到y轴两边的阴影部分关于y轴对称，由定积分的法则得到由两条曲线y=1，y=4，y=x2所围成的图形的面积．
解答：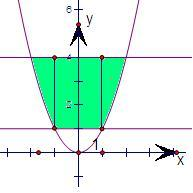
解：如图，
由曲线y=1，y=4，y=x2所围成的平面图形为阴影部分，
因为y轴两边的阴影部分关于y轴对称，而右边的部分分成一个小矩形与曲线三角形进行计算，
所以S=2（1×2+∫12（4-x2）dx=4+2（4x-
）|12=
，
故答案为：
．
解：如图，由曲线y=1，y=4，y=x2所围成的平面图形为阴影部分，
因为y轴两边的阴影部分关于y轴对称，而右边的部分分成一个小矩形与曲线三角形进行计算，
所以S=2（1×2+∫12（4-x2）dx=4+2（4x-
| x3 |
| 3 |
| 28 |
| 3 |
故答案为：
| 28 |
| 3 |
点评：考查学生会利用定积分求图形面积的能力，同时考查了计算能力，属于中档题．
练习册系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
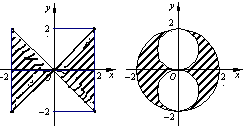（理）由曲线y=|x|，y=-|x|，x=2，x=-2围成的图形绕y轴旋转一周所得的旋转体的体积为V1；满足x2+y2≤4，x2+（y-1）2≥1，x2+（y+1）2≥1的点组成的图形绕y轴旋转一周所得的旋转体的体积为V2，试写出V1与V2的一个关系式V1：V2=