题目内容
 已知△ABC和△DBC所在的平面互相垂直,且AB=BC=BD,∠CBA=∠DBC=120°,求
已知△ABC和△DBC所在的平面互相垂直,且AB=BC=BD,∠CBA=∠DBC=120°,求(1)直线AD与平面BCD所成角的大小;
(2)直线AD与直线BC所成角的大小;
(3)二面角A-BD-C的余弦值.
分析:(1)作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,通过求
与平面BCD的夹角去求.
(2)通过
与
的夹角去求.
(3)求出平面CBD的一个法向量为
以及平面ABD的一个法向量为
,求出两法向量的余弦值即可得到平面CDF与平面ABCD所成角的余弦值.
| AD |
(2)通过
| AD |
| BC |
(3)求出平面CBD的一个法向量为
| n1 |
| n2 |
解答:解:(1)设AB=1,作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,得下列坐标: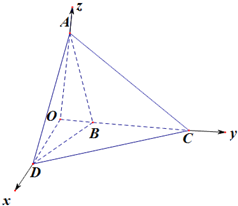
O(0,0,0)D(
,0,0)B(0,
,0)C(0,
,0)A(0,0,
)
=(
,0,-
),显然
=(0,0,1)为平面BCD的一个法向量
|cos<
,
>|=|
|=|-
|=
∴,直线AD与平面BCD所成角的大小90°-45°=45°
(2)
•
=(
,0,-
)•(0,1,0)=0
所以AD与BC所成角等于90°.
(3)设平面ABD的法向量为
=(x,y,1)则
(x,y,1)•
=(x,y,1)•(0,
, -
)=0
(x,y,1)•
=(x,y,1)•(
,0,-
)=0
解得 x=1,y=
,
则
=(1,
,1)
显然(0,0,1)为平面BCD的法向量.
设二面角A-BD-C大小为θ,则|cosθ|=
=
=
又二面角A-BD-C为钝二面角,因此,二面角的余弦为-
.

O(0,0,0)D(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| AD |
| ||
| 2 |
| ||
| 2 |
| n1 |
|cos<
| AD |
| n1 |
-
| ||||
|
| ||
| 2 |
| ||
| 2 |
∴,直线AD与平面BCD所成角的大小90°-45°=45°
(2)
| AD |
| BC |
| ||
| 2 |
| ||
| 2 |
所以AD与BC所成角等于90°.
(3)设平面ABD的法向量为
| n2 |
(x,y,1)•
| AB |
| 1 |
| 2 |
| ||
| 2 |
(x,y,1)•
| AD |
| ||
| 2 |
| ||
| 2 |
解得 x=1,y=
| 3 |
则
| n2 |
| 3 |
显然(0,0,1)为平面BCD的法向量.
设二面角A-BD-C大小为θ,则|cosθ|=
| ||||
|
|
| 1 | ||
1×
|
| ||
| 5 |
又二面角A-BD-C为钝二面角,因此,二面角的余弦为-
| ||
| 5 |
点评:本题考查空间角的计算,二面角求解,考查转化的思想方法,计算能力.利用空间向量的知识,则使问题论证变成了代数运算,使人们解决问题更加方便.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,BC=3SA=3AB=3AD.
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,BC=3SA=3AB=3AD. A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.
A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.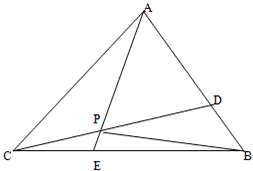 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使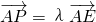 ,
,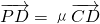 ,
,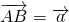 ,
,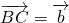 .
. ,
, 表示
表示 ;
; +
+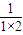 +
+ +L+
+L+ <2.
<2.