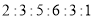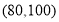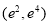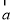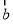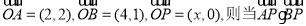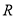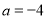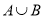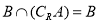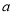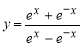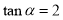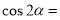题目内容
已知函数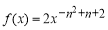
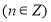 满足
满足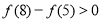 .
.
(1)求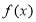 的解析式;
的解析式;
(2)对于(1)中得到的函数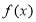 ,试判断是否存在
,试判断是否存在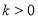 ,使
,使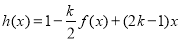 在区间
在区间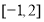 上的值域为
上的值域为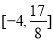 ?若存在,求出
?若存在,求出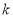 ;若不存在,请说明理由.
;若不存在,请说明理由.
(1) ;(2)存在
;(2)存在 满足条件
满足条件
【解析】
试题分析:(1)由条件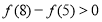 结合幂函数的图像与性质可知
结合幂函数的图像与性质可知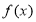 在第一象限单调递增,从而可得
在第一象限单调递增,从而可得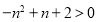 ,解出
,解出 的整数解即可得到函数的解析式;(2)先假设存在
的整数解即可得到函数的解析式;(2)先假设存在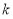 的值满足题意,然后根据二次函数取得最值的位置:区间的端点与对称轴的位置,进行确定
的值满足题意,然后根据二次函数取得最值的位置:区间的端点与对称轴的位置,进行确定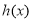 在什么位置取得最大值与最小值,最后根据题目所给的最值即可得到参数
在什么位置取得最大值与最小值,最后根据题目所给的最值即可得到参数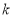 的值.
的值.
试题解析:(1) ,由幂函数的性质可知,
,由幂函数的性质可知,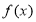 在第一象限为增函数
在第一象限为增函数
 ,得
,得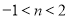 ,又由
,又由 ,所以
,所以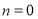 或
或 5分
5分
 6分
6分
(2)假设存在 满足条件,由已知
满足条件,由已知 8分
8分
而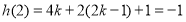 9分
9分
所以两个最值点只能在端点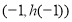 和顶点
和顶点 处取得
处取得
而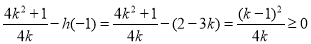 11分
11分
 且
且
解得 13分
13分
 存在
存在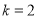 满足条件 14分.
满足条件 14分.
考点:幂函数及二次函数的单调性与最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目