题目内容
已知函数
(1)求函数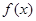 的最小值及单调减区间;
的最小值及单调减区间;
(2)在
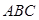 中,
中,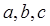 分别是角
分别是角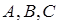 的对边,且
的对边,且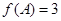 ,
,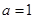 ,
,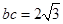 ,且
,且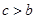 ,求
,求 ,c的值
,c的值
【答案】
(1)最小值为-1,单调减区间为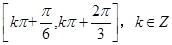 ;(2)
;(2)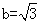 ,
, 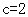
【解析】
试题分析:(1)因为已知函数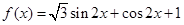 通过化一公式函数
通过化一公式函数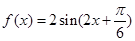 .又因为函数
.又因为函数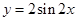 的单调递减区间是
的单调递减区间是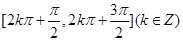 .所以可得
.所以可得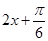 在该区间内的范围即可求得
在该区间内的范围即可求得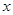 的范围.
的范围.
(2)因为在
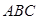 中,
中,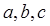 分别是角
分别是角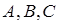 的对边,且
的对边,且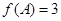 由(1)式可求得角A的值.再利用余弦定理即可得可求得三角形中的边
由(1)式可求得角A的值.再利用余弦定理即可得可求得三角形中的边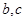 的关系.从而即可求出
的关系.从而即可求出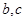 的值.
的值.
试题解析:(1)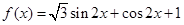
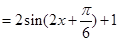
∴函数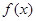 的最小值为
的最小值为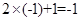
由 得:
得:
单调减区间为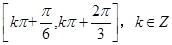 6分
6分
(2)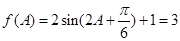
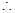
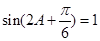
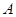 是三角形内角,∴
是三角形内角,∴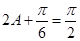
即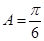
∴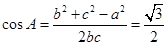 即:
即: .
.
将 代入可得:
代入可得: ,解之得:
,解之得: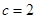 或
或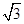 .
.
∴, 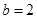 或
或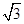
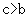 , ∴
, ∴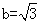 ,
,
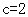 , 13分
, 13分
考点:1.三角函数的化一公式.2.三角函数的单调性.3.解三角形.4.余弦定理.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
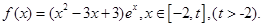
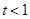 时,求函数
时,求函数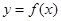 的单调区间;
的单调区间;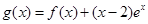 ,试问函数
,试问函数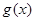 在
在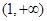 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
 的定义域;
的定义域; 为何值时,函数值大于1.
为何值时,函数值大于1.
 ,
, ,
, ,
, 这几个函数值,你能发现f(x)与
这几个函数值,你能发现f(x)与 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;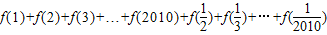 的值;
的值; 在区间(0,+∞)上的单调性.
在区间(0,+∞)上的单调性.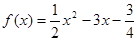
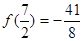 ,求
,求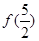
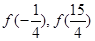 的大小
的大小