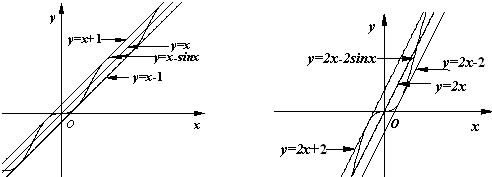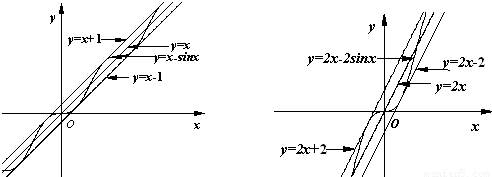题目内容
设直线l:y=g(x),曲线S:y=F(x).若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有g(x)≥F(x).则称直线l为曲线S的“上夹线”.
(Ⅰ)已知函数f(x)=x-2sinx.求证:y=x+2为曲线f(x)的“上夹线”.
(Ⅱ)观察下图:
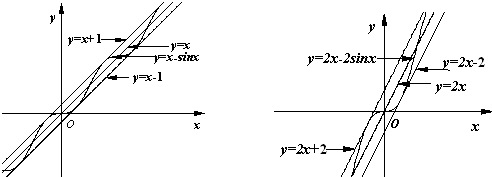
根据上图,试推测曲线S:y=mx-nsinx(n>0)的“上夹线”的方程,并给出证明.
(Ⅰ)已知函数f(x)=x-2sinx.求证:y=x+2为曲线f(x)的“上夹线”.
(Ⅱ)观察下图:
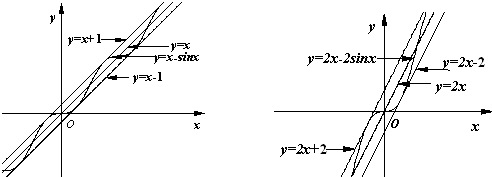
根据上图,试推测曲线S:y=mx-nsinx(n>0)的“上夹线”的方程,并给出证明.
解(Ⅰ)由f'(x)=1-2cosx=1得cosx=0,(1分)
当x=-
时,cosx=0,
此时y1=x+2=-
+2,y2=x-2sinx=-
+2,(2分)
y1=y2,所以(-
,-
+2)是直线l与曲线S的一个切点;(3分)
当x=
时,cosx=0,
此时y1=x+2=
+2,y2=x-2sinx=
+2,(4分)
y1=y2,,所以(
,
+2)是直线l与曲线S的一个切点;(5分)
所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,g(x)-F(x)=(x+2)-(x-2sinx)=2+2sinx≥0,
所以g(x)≥F(x)(6分)
因此直线l:y=x+2是曲线S:y=ax+bsinx的“上夹线”.(7分)
(Ⅱ)推测:y=mx-nsinx(n>0)的“上夹线”的方程为y=mx+n(9分)
①先检验直线y=mx+n与曲线y=mx-nsinx相切,且至少有两个切点:设:F(x)=mx-nsinx
∵F'(x)=m-ncosx,令F'(x)=m-ncosx=m,得:x=2kπ±
(k∈Z)(10分)
当x=2kπ-
时,F(2kπ-
)=m(2kπ-
)+n
故:过曲线F(x)=mx-nsinx上的点2kπ-
,m(2kπ-
)+n)的切线方程为:
y-[m(2kπ-
)+n]=m[-(2kπ-
)],化简得:y=mx+n.
即直线y=mx+n与曲线y=F(x)=mx-nsinx相切且有无数个切点.(12分)
不妨设g(x)=mx+n
②下面检验g(x)≥F(x)
∵g(x)-F(x)=m(1+sinx)≥0(n>0)
∴直线y=mx+n是曲线y=F(x)=mx-nsinx的“上夹线”.(14分)
当x=-
| π |
| 2 |
此时y1=x+2=-
| π |
| 2 |
| π |
| 2 |
y1=y2,所以(-
| π |
| 2 |
| π |
| 2 |
当x=
| 3π |
| 2 |
此时y1=x+2=
| 3π |
| 2 |
| 3π |
| 2 |
y1=y2,,所以(
| 3π |
| 2 |
| 3π |
| 2 |
所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,g(x)-F(x)=(x+2)-(x-2sinx)=2+2sinx≥0,
所以g(x)≥F(x)(6分)
因此直线l:y=x+2是曲线S:y=ax+bsinx的“上夹线”.(7分)
(Ⅱ)推测:y=mx-nsinx(n>0)的“上夹线”的方程为y=mx+n(9分)
①先检验直线y=mx+n与曲线y=mx-nsinx相切,且至少有两个切点:设:F(x)=mx-nsinx
∵F'(x)=m-ncosx,令F'(x)=m-ncosx=m,得:x=2kπ±
| π |
| 2 |
当x=2kπ-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故:过曲线F(x)=mx-nsinx上的点2kπ-
| π |
| 2 |
| π |
| 2 |
y-[m(2kπ-
| π |
| 2 |
| π |
| 2 |
即直线y=mx+n与曲线y=F(x)=mx-nsinx相切且有无数个切点.(12分)
不妨设g(x)=mx+n
②下面检验g(x)≥F(x)
∵g(x)-F(x)=m(1+sinx)≥0(n>0)
∴直线y=mx+n是曲线y=F(x)=mx-nsinx的“上夹线”.(14分)

练习册系列答案
相关题目