题目内容
已知双曲线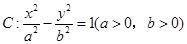 ,
, 是右顶点,
是右顶点, 是右焦点,点
是右焦点,点 在
在 轴的正半轴上,且满足
轴的正半轴上,且满足 ,
,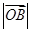 ,
, 成等比数列,过
成等比数列,过 作双曲线
作双曲线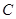 在第一、三象限的渐近线的垂线
在第一、三象限的渐近线的垂线 ,垂足为
,垂足为 .
.

(1)求证: ;
;
(2)若直线 与双曲线
与双曲线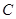 的左、右两支分别相交于点
的左、右两支分别相交于点 ,求双曲线
,求双曲线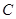 的离心率
的离心率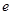 的取值范围.
的取值范围.
【答案】
(1)证明:见解析。(2)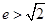 .
.
【解析】
试题分析:(1)证明:直线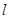 为
为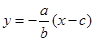 , ①
, ①
在第一、三象限的渐近线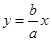 , ②
, ②
解①、②得垂足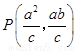 .
.
因为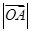 ,
,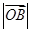 ,
,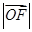 成等比数列,
成等比数列,
所以可得点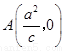 .
.
所以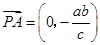 ,
,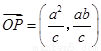 ,
,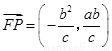 .
.
所以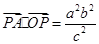 ,
,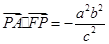 .
.
因此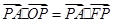 ;
;
(2)解:由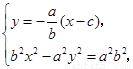 得
得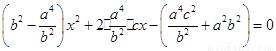 ,
,
因为直线 与双曲线
与双曲线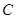 的左、右两支分别相交于点
的左、右两支分别相交于点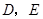 ,
,
所以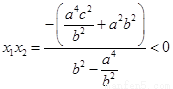 ,
,
所以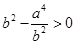 ,即
,即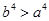 ,
,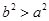 ,
,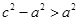 ,
,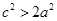 ,
,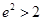 ,
,
因此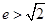 .
.
考点:本题主要考查直线与双曲线位置关系,双曲线的几何性质,等差数列基础知识,平面向量的数量积。
点评:综合性较强,在高考题中具有方向性。数形结合,综合应用韦达定理。

练习册系列答案
相关题目
 :
: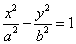
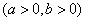 的右焦点是
的右焦点是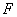 ,右顶点是
,右顶点是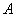 ,虚轴的上端点是
,虚轴的上端点是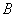 ,且
,且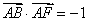 ,
,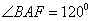 .
.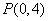 的直线
的直线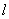 交双曲线于
交双曲线于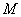 、
、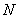 两点,交
两点,交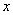 轴于点
轴于点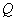 (点
(点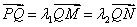 ,且
,且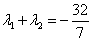 时,求点
时,求点