题目内容
已知A是△BCD所在平面外的点,∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.
(1)求证:AB⊥CD; (2)求AB与平面BCD所成角的余弦值.
(1)求证:AB⊥CD; (2)求AB与平面BCD所成角的余弦值.
(1)∵∠BAC=∠CAD=∠DAB=60°, AC=AD=2,AB=3, ∴△ABC≌△ABD,BC=BD.取CD的中点M,连AM、BM,则CD⊥AM,CD⊥BM. ∴CD⊥平面ABM,于是AB⊥BD.
(2)过A作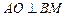 于O,∵CD⊥平面ABM,∴CD⊥AO,∴AO⊥面BCD,
于O,∵CD⊥平面ABM,∴CD⊥AO,∴AO⊥面BCD,
∴BM是AB在面BCD内的射影,这样∠ABM是AB与平面BCD所成的角.
在△ABC中,AB=3,AC=2,∠BAC=60°,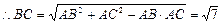 .
.
在△ACD中, AC=AD=2,∠CAD=60°,∴△ACD是正三角形,AM=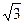 .
.
在Rt△BCM中,BC=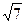 ,CM=1,
,CM=1,
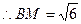 .
.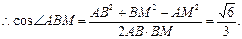
(2)过A作
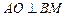 于O,∵CD⊥平面ABM,∴CD⊥AO,∴AO⊥面BCD,
于O,∵CD⊥平面ABM,∴CD⊥AO,∴AO⊥面BCD,∴BM是AB在面BCD内的射影,这样∠ABM是AB与平面BCD所成的角.
在△ABC中,AB=3,AC=2,∠BAC=60°,
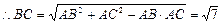 .
. 在△ACD中, AC=AD=2,∠CAD=60°,∴△ACD是正三角形,AM=
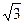 .
. 在Rt△BCM中,BC=
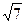 ,CM=1,
,CM=1,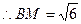 .
.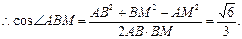
略

练习册系列答案
相关题目



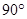
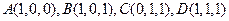 ,求直线AD与平面
,求直线AD与平面 的夹
的夹 角。
角。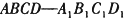 中,M为
中,M为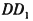 的中
的中 点,0为底面ABCD的中心,P为棱
点,0为底面ABCD的中心,P为棱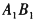 的中点,则直线OP与直线AM所成的角是
的中点,则直线OP与直线AM所成的角是



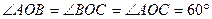 ,则交线OA与平面OBC所成的角的余弦值是( )
,则交线OA与平面OBC所成的角的余弦值是( ) B.
B. C.
C. D.
D.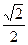
 中,
中, 是
是 的中点,
的中点, 是底面
是底面 的中心,
的中心,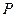 是
是 上的任意点,则直线与所成的角为
上的任意点,则直线与所成的角为 
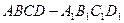 中,
中,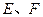 分别是棱
分别是棱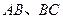 的中点,则直线
的中点,则直线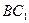 与直线
与直线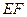 所成角为___
所成角为___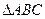 沿DE、EF、DF折成三棱锥P—DEF,如图所示,则异面直线PG与MN所成角的大小为 ▲
沿DE、EF、DF折成三棱锥P—DEF,如图所示,则异面直线PG与MN所成角的大小为 ▲ 