题目内容
17.直线xcosθ+y-m=0(θ∈R)的倾斜角α的范围是( )| A. | [0,π] | B. | [$\frac{π}{4},\frac{3π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | D. | [$\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{3π}{4}$] |
分析 由直线xcosθ+y-m=0的斜率k=-cosθ∈[-1,1],得-1≤tanα<0或0≤tanα≤1,由此能求出直线xcosθ+y-m=0的倾斜角范围.
解答 解:直线xcosθ+y+m=0的斜率k=-cosθ∈[-1,1],
∴-1≤tanα<0或0≤tanα≤1,
∴$\frac{3π}{4}$≤α<π或0≤α≤$\frac{π}{4}$.
∴直线xcosθ+y+m=0的倾斜角范围是[0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π).
故选:C.
点评 本题考查直线的倾斜角的取值范围的求法,是基础题,解题时要注意直线的斜率的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.关于复数z=$\frac{2}{-1+i}$的四个命题:
p1:复数z对应的点在第二象限,
p2:z2=2i,
p3:z的共轭复数为1+i,
p4:z的虚部为-1.
其中的真命题个数为( )
p1:复数z对应的点在第二象限,
p2:z2=2i,
p3:z的共轭复数为1+i,
p4:z的虚部为-1.
其中的真命题个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.如框图,当x1=5,x2=8,p=8.5时,x3=( )
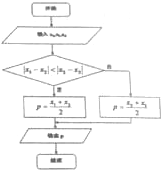

| A. | 6 | B. | 7 | C. | 9 | D. | 10 |
9.过曲线C:y=$\frac{1}{x}$(x>0)上一点P(x0,y0)作曲线C的切线,若切线的斜率为-4,则x0等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{4}$ |
6.在等比数列{an}(n∈N*)中,若a1=1,a4=$\frac{1}{8}$,则该数列的前10项和为( )
| A. | 2-$\frac{1}{2^4}$ | B. | 2-$\frac{1}{{2}^{9}}$ | C. | 2-$\frac{1}{{{2^{10}}}}$ | D. | 2-$\frac{1}{{{2^{11}}}}$ |
7.下列幂函数中,过点(0,0),(1,1)的偶函数是( )
| A. | y=x${\;}^{\frac{1}{2}}$ | B. | y=x${\;}^{\frac{1}{3}}$ | C. | y=x-2 | D. | y=x4 |