题目内容
已知函数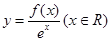 满足
满足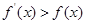 ,则
,则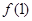 与
与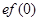 大小关系是( )
大小关系是( )
A.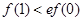 | B.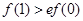 | C.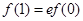 | D.不能确定 |
B
解析试题分析: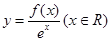 求导数得
求导数得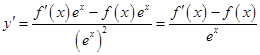
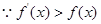 所以
所以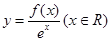 是增函数
是增函数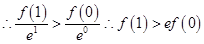
考点:导数判定单调性
点评:首先对原函数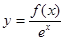 求导,通过判断导数正负得到其单调性,进而利用单调性比较大小
求导,通过判断导数正负得到其单调性,进而利用单调性比较大小

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
.设三次函数 的导函数为
的导函数为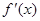 ,函数
,函数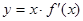 的图象的一部分如图所示,则正确的是
的图象的一部分如图所示,则正确的是 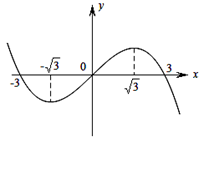
A. 的极大值为 的极大值为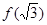 ,极小值为 ,极小值为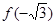 |
B. 的极大值为 的极大值为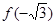 ,极小值为 ,极小值为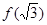 |
C. 的极大值为 的极大值为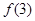 ,极小值为 ,极小值为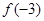 |
D. 的极大值为 的极大值为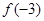 ,极小值为 ,极小值为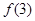 |
曲线y=x3-3x2+1在点(1,-1)处的切线方程为( )
| A.y=3x-4 | B.y=4x-5 |
| C.y=-4x+3 | D. y=-3x+2 |
已知函数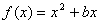 的图像在点
的图像在点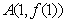 处的切线的斜率为3,数列
处的切线的斜率为3,数列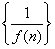 的前
的前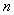 项和为
项和为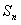 ,则
,则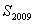 的值为( )
的值为( )
A.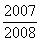 | B.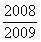 | C.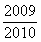 | D.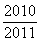 |
已知函数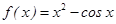 ,则
,则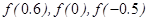 的大小关系是( )
的大小关系是( )
A.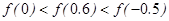 | B. |
C.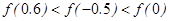 | D. |
 =( )
=( )
A. | B.2 | C. | D. |
函数 的导函数为( )
的导函数为( )
A. | B.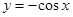 | C.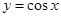 | D.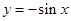 |
已知定义在 上的奇函数
上的奇函数 ,若
,若 的导函数
的导函数 满足
满足 则不等式
则不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
函数f(x)=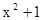 在(1,2)处的切线斜率为( )
在(1,2)处的切线斜率为( )
| A.1 | B.2 | C.3 | D.4 |