题目内容

函数f（x）=
|x3+1|，(|x|＞1)
2sin
π
2
x，(|x|＜1)
，则下列结论正确的是（　　）
A、函数f（x）在[-1，+∞]上为增函数
B、函数f（x）的最小正周期为4
C、函数f（x）是奇函数
D、函数f（x）无最小值
分析：先画出函数f（x）=
|x3+1|，(|x|＞1)
2sin
π
2
x，(|x|＜1)
的图象，观察图象对选项一一验证即可．
解答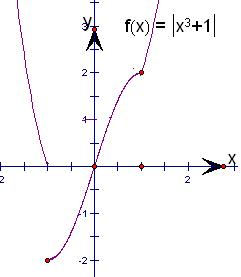：精英家教网解：画出函数f（x）=
|x3+1|，(|x|＞1)
2sin
π
2
x，(|x|＜1)
，的图象，如图．
观察图象可得：
函数f（x）在[-1，+∞]上不为增函数，故A错；
函数f（x）的不是周期函数，故B错；
函数f（x）的图象不关于原点对称，不是奇函数，故C错；
函数f（x）无最小值，D正确．
故选D．
点评：本题主要考查了分段函数的解析式求法及其图象的作法，以及函数的性质．考查了数形结合的思想方法．属于基础题．
练习册系列答案
相关题目
已知函数f（x）=-x3+ax2+bx+c在（-∞，0）上是减函数，在（0，1）上是增函数，函数f（x）在R上有三个零点．
（1）求b的值；
（2）若1是其中一个零点，求f（2）的取值范围；
（3）若a=1，g（x）=f′（x）+3x2+lnx，试问过点（2，5）可作多少条直线与曲线y=g（x）相切？请说明理由．
（2007•东城区一模）已知函数f（x）=x3+ax2+bx+c，曲线y=f（x）在点x=1处的切线l不过第四象限且斜率为3，又坐标原点到切线l的距离为
10
10
，若x=
2
3
时，y=f（x）有极值．
（1）求a，b，c的值；
（2）求y=f（x）在[-3，1]上的最大值和最小值．
（2013•宁波模拟）已知函数f（x）=x3+ax2-a2x+2，a∈R．
（1）若a＜0时，试求函数y=f（x）的单调递减区间；
（2）若a=0，且曲线y=f（x）在点A、B（A、B不重合）处切线的交点位于直线x=2上，证明：A、B 两点的横坐标之和小于4；
（3）如果对于一切x1、x2、x3∈[0，1]，总存在以f（x1）、f（x2）、f（x3）为三边长的三角形，试求正实数a的取值范围．
设函数f（x）=x3-3ax+b（a≠0），已知曲线y=f（x）在点（2，f（x））处在直线y=8相切．
（Ⅰ）求a，b的值；
（Ⅱ）求函数f（x）的单调区间与极值点．
对于函数f（x）=x3+ax2-x+1的极值情况，4位同学有下列说法：甲：该函数必有2个极值；乙：该函数的极大值必大于1；丙：该函数的极小值必小于1；丁：方程f（x）=0一定有三个不等的实数根． 这四种说法中，正确的个数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网