题目内容
已知函数f(x)=logax(a>0,a≠1),且f(3)-f(2)=1.
(1)若f(3m-2)<f(2m+5),求实数m的取值范围;
(2)求使f(x-
)=log
成立的x的值.
(1)若f(3m-2)<f(2m+5),求实数m的取值范围;
(2)求使f(x-
| 2 |
| x |
| 3 |
| 2 |
| 7 |
| 2 |
∵f(3)-f(2)=1,
∴f(3)-f(2)=loga3-loga2=loga
=1,
∴a=
.
(1)∵a=
.
∴函数f(x)=log
x在定义域(0,+∞)上单调递增,
若f(3m-2)<f(2m+5),
则
,即
,
∴
<m<7.
(2)若f(x-
)=log
=f(
),
则x-
=
,
∴x=-
或x=4满足条件.
∴f(3)-f(2)=loga3-loga2=loga
| 3 |
| 2 |
∴a=
| 3 |
| 2 |
(1)∵a=
| 3 |
| 2 |
∴函数f(x)=log
| 3 |
| 2 |
若f(3m-2)<f(2m+5),
则
|
|
∴
| 2 |
| 3 |
(2)若f(x-
| 2 |
| x |
| 3 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
则x-
| 2 |
| x |
| 7 |
| 2 |
∴x=-
| 1 |
| 2 |

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
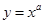 的图象过点
的图象过点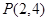 ,则图中阴影部分的面积等于 .
,则图中阴影部分的面积等于 .