题目内容
设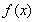 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, .若对任意的
.若对任意的 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的最大值是( )
的最大值是( )
A. B.
B. C.
C. D.2
D.2
【答案】
C
【解析】
试题分析:由于 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, ,
, ,且
,且 在
在 单调递增,
单调递增,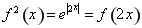 ,
, ,即
,即 ,可得
,可得 ,解得
,解得 或
或 ,对任意的
,对任意的 ,不等式
,不等式 恒成立,即
恒成立,即 或
或 ,解得
,解得 ,故实数
,故实数 的最大值是
的最大值是 .
.
考点:奇偶性与单调性的综合,函数恒成立问题.

练习册系列答案
相关题目
 是定义在
是定义在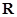 上的偶函数,对任意的
上的偶函数,对任意的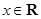 ,都有
,都有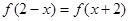 ,且当
,且当 时,
时, ,若关于
,若关于 的方程
的方程
 在区间
在区间 内恰有三个不同实根,则实数
内恰有三个不同实根,则实数 的取值范围是 .
的取值范围是 . 是定义在
是定义在 上的偶函数,对任意的
上的偶函数,对任意的 ,都有
,都有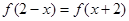 ,且当
,且当 时,
时, ,若关于
,若关于 的方程
的方程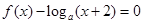
 在区间
在区间 内恰有三个不同实根,则实数
内恰有三个不同实根,则实数 的取值范围是
.
的取值范围是
. 是定义在
是定义在 上的偶函数,且
上的偶函数,且 ,当
,当 时,
时, ,若在区间
,若在区间 内关于
内关于 的方程
的方程 ,恰有
,恰有 个不同的实数根,则实数
个不同的实数根,则实数
 的取值范围是
的取值范围是 B.
B. C.
C.  D.
D.
 是定义在
是定义在 上的偶函数,对任意
上的偶函数,对任意 ,都有
,都有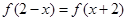 成立,且当
成立,且当 时,
时, .若关于
.若关于 的方程
的方程
 在区间
在区间 内恰有两个不同实根,则实数
内恰有两个不同实根,则实数 的取值范围是
.
的取值范围是
.