题目内容
设 是定义在
是定义在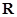 上的偶函数,对任意的
上的偶函数,对任意的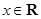 ,都有
,都有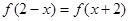 ,且当
,且当 时,
时, ,若关于
,若关于 的方程
的方程
 在区间
在区间 内恰有三个不同实根,则实数
内恰有三个不同实根,则实数 的取值范围是 .
的取值范围是 .
【答案】
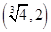
【解析】解:设x∈[0,2],则-x∈[-2,0],∴f(-x)=(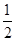 )-x-1=2x-1,
)-x-1=2x-1,
∵f(x)是定义在R上的偶函数,∴f(x)=f(-x)=2x-1.
∵对任意x∈R,都有f(x)=f(x+4),
∴当x∈[2,4]时,(x-4)∈[-2,0],∴f(x)=f(x-4)=(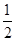 )x-4-1;
)x-4-1;
及当x∈[4,6]时,(x-4)∈[0,2],∴f(x)=f(x-4)=2x-4-1.
∵若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,
∴函数y=f(x)与函数y=loga(x+2)在区间(-2,6]上恰有三个交点,通过画图可知:恰有三个交点的条件是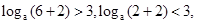 得到参数a的范围是
得到参数a的范围是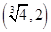 ,故答案为
,故答案为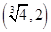

练习册系列答案
相关题目
 是定义在
是定义在 上的偶函数,对任意的
上的偶函数,对任意的 ,都有
,都有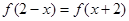 ,且当
,且当 时,
时, ,若关于
,若关于 的方程
的方程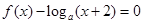
 在区间
在区间 内恰有三个不同实根,则实数
内恰有三个不同实根,则实数 的取值范围是
.
的取值范围是
. 是定义在
是定义在 上的偶函数,且
上的偶函数,且 ,当
,当 时,
时, ,若在区间
,若在区间 内关于
内关于 的方程
的方程 ,恰有
,恰有 个不同的实数根,则实数
个不同的实数根,则实数
 的取值范围是
的取值范围是 B.
B. C.
C.  D.
D.
 是定义在
是定义在 上的偶函数,对任意
上的偶函数,对任意 ,都有
,都有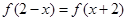 成立,且当
成立,且当 时,
时, .若关于
.若关于 的方程
的方程
 在区间
在区间 内恰有两个不同实根,则实数
内恰有两个不同实根,则实数 的取值范围是
.
的取值范围是
.