题目内容
为了某班学生喜爱打篮球是否与性别有关,对本班50人进行问卷调查得到了如下的列联表:
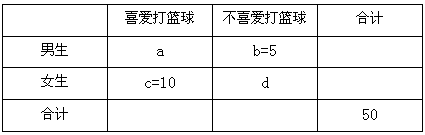
已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为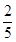 .
.
(1)请将上面的列联表补充完整;
(2)是否有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关;请说明理由.
附参考公式: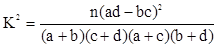

已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为
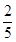 .
.(1)请将上面的列联表补充完整;
(2)是否有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关;请说明理由.
附参考公式:
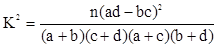
P(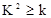 ) ) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
解:∵已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为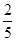
∴不爱打篮球的学生共有本质区别50×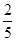 =20人
=20人
(1)列联表补充如下:
(2)∵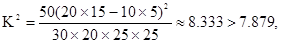
∴有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
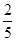
∴不爱打篮球的学生共有本质区别50×
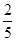 =20人
=20人(1)列联表补充如下:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | A+20 | b=5 | 25 |
| 女生 | c=10 | d=15 | 25 |
| 合计 | 30 | 20 | 50 |
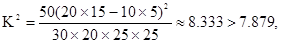
∴有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
本试题主要是考查了古典概型概率的求解和独立性检验的思想的运用。
(1)因为已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为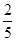 ,则可知结论。
,则可知结论。
(2)因为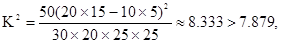 ,那么可以把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
,那么可以把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
(1)因为已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为
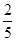 ,则可知结论。
,则可知结论。(2)因为
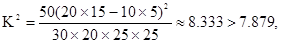 ,那么可以把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
,那么可以把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
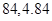
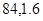
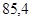
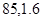
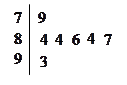
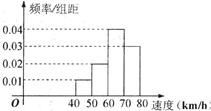
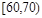 则速度在 的汽车大约有( )
则速度在 的汽车大约有( ) 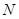 名师生志愿者,现将所有志愿者按年龄情况分为
名师生志愿者,现将所有志愿者按年龄情况分为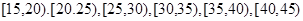 等六组,其频率分布直方图如下图所示: 已知
等六组,其频率分布直方图如下图所示: 已知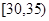 之间的志愿者共
之间的志愿者共 人.
人.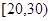 之间的志愿者人数
之间的志愿者人数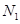 ;
;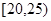 和
和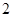 名数学教师,现从这两个组中各选取
名数学教师,现从这两个组中各选取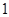 名数学教师的概率?
名数学教师的概率?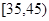 之间的志愿者(其中共有
之间的志愿者(其中共有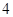 名女教师,其余全为男教师)中随机选取
名女教师,其余全为男教师)中随机选取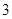 名担任后勤保障工作,其中女教师的人数为
名担任后勤保障工作,其中女教师的人数为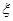 ,求
,求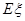 .
.
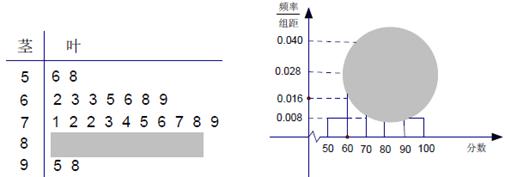
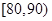 之间的频数;
之间的频数;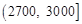 的频率为 __________.
的频率为 __________.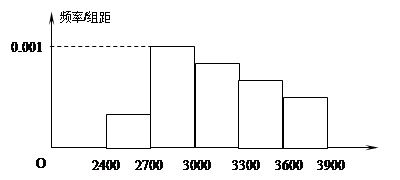

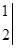
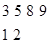 ,则该组数据的中位数为 .
,则该组数据的中位数为 .