题目内容
(本小题满分14分)
已知函数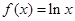 ,
,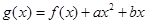 ,函数
,函数 的图象在点
的图象在点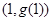 处的切线平行于
处的切线平行于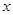 轴.
轴.
(1)确定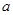 与
与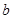 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意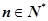 ,都有
,都有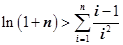 成立.
成立.
(1)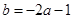
(2)当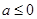 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在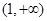 单调递减;
单调递减;
当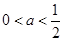 时,函数
时,函数 在
在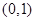 单调递增,在
单调递增,在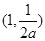 单调递减;在
单调递减;在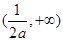 上单调递增;
上单调递增;
当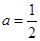 时,函数
时,函数 在
在 上单调递增,
上单调递增,
当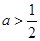 时,函数
时,函数 在
在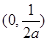 上单调递增,在
上单调递增,在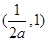 单调递减;在
单调递减;在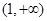 上单调递增.
上单调递增.
(3)可以利用放缩不等式证明也可以构造新数列利用数列的性质证明还可以构造函数利用导数证明
解析试题分析:(1)依题意得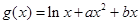 ,则
,则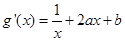
由函数 的图象在点
的图象在点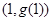 处的切线平行于
处的切线平行于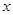 轴得:
轴得: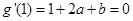
 ∴
∴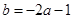 ……3分
……3分
(2)由(1)得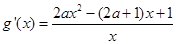
 ……4分
……4分
∵函数 的定义域为
的定义域为
∴当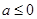 时,
时,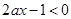 在
在 上恒成立,
上恒成立,
由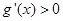 得
得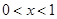 ,由
,由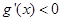 得
得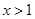 ,
,
即函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在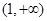 单调递减; ……5分
单调递减; ……5分
当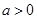 时,令
时,令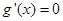 得
得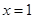 或
或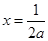 ,
,
若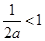 ,即
,即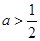 时,
时,
由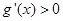 得
得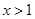 或
或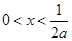 ,由
,由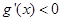 得
得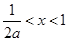 ,
,
即函数 在
在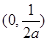 ,
,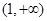 上单调递增,在
上单调递增,在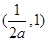 单调递减; ……6分
单调递减; ……6分
若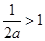 ,即
,即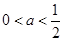 时,
时,
由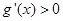 得
得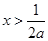 或
或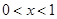 ,由
,由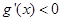 得
得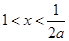 ,
,
即函数 在
在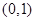 ,
,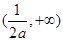 上单调递增,在
上单调递增,在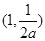 单调递减; ……7分
单调递减; ……7分
若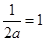 ,即
,即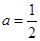 时,在
时,在 上恒有
上恒有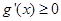 ,
,
即函数 在
在 上单调递增, ……8分
上单调递增, ……8分
综上得:当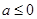 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在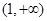 单调递减;
单调递减;
当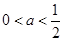 时,函数
时,函数 在
在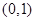 单调递增,在
单调递增,在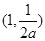 单调递减;在
单调递减;在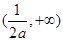 上单调递增;
上单调递增;
当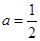 时,函数
时,函数 在
在
练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
 的定义域;(6分)
的定义域;(6分) 在
在 上的值域.(6分)
上的值域.(6分) 的最大值.
的最大值.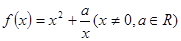
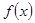 的奇偶性;
的奇偶性;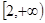 是增函数,求实数
是增函数,求实数 的取值范围。
的取值范围。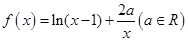
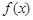 的单调区间;
的单调区间;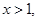 且
且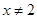 时,
时,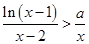 恒成立,求实数
恒成立,求实数 的范围.
的范围.
 的最小正周期.
的最小正周期. 时,求函数
时,求函数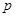 与死亡年数
与死亡年数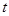 之间的函数关系式;
之间的函数关系式; )
)
 的不等式
的不等式 ;
; 的图象恒在函数
的图象恒在函数 图象的上方(没有公共点),求
图象的上方(没有公共点),求 的取值范围。
的取值范围。 元,若销售价为
元,若销售价为 元,可卖出
元,可卖出 元,销售量就减少
元,销售量就减少