题目内容
(本小题满分10分)已知命题p:函数 在R上是减函数;命题q:在平面直角坐标系中,点
在R上是减函数;命题q:在平面直角坐标系中,点 在直线
在直线 的左下方。若
的左下方。若 为假,
为假, 为真,求实数
为真,求实数 的取值范围
的取值范围
【答案】
(-3,4)
【解析】
试题分析:解:f ′(x)=3ax2+6x-1,∵函数f(x)在R上是减函数,
∴f ′(x)≤0即3ax2+6x-1≤0(x∈R).
(1)当a=0时,f ′(x)≤0,对x∈R不恒成立,故a≠0.
(2)当a≠0时,要使3ax2+6x-1≤0对x∈R恒成立,
应满足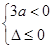 ,即
,即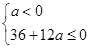 ,∴p:a≤-3. …………5分
,∴p:a≤-3. …………5分
由在平面直角坐标系中,点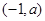 在直线
在直线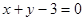 的左下方,
的左下方,
得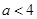 ∴q:
∴q: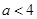 , …………7分
, …………7分
 :a≤-3;
:a≤-3; :
: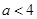
综上所述,a的取值范围是(-3,4).…………10分
考点:本试题考查了命题的真值,函数性质。
点评:解决该试题的关键是利用函数单调性和二元一次不等式的表示的区域可知a的范围。细节是理解且为真,或为假,得到必有一真一假,得到参数的范围,属于中档题。

练习册系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,