题目内容
4.已知函数f(x)=log2($\frac{x+b}{x-b}$),(b≠0).(1)求f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)解关于x的不等式f(x)≥1.
分析 (1)根据对数函数的真数大于0,构造不等式,对b值分类讨论,可得不同情况下函数的定义域;
(2)根据奇函数的定义,可判断出函数f(x)为奇函数,
(3)若f(x)≥1,则$\frac{x+b}{x-b}$≥2,对b值分类讨论,可得不同情况下不等式的解集.
解答 解:(1)当b<0时,由$\frac{x+b}{x-b}$>0得:x∈(-∞,b)∪(-b,+∞),故此时函数的定义域为:(-∞,b)∪(-b,+∞),
当b>0时,由$\frac{x+b}{x-b}$>0得:x∈(-∞,-b)∪(b,+∞),故此时函数的定义域为:(-∞,-b)∪(b,+∞),
(2)由(1)得函数的定义域关于原点对称,
又由f(-x)=log2($\frac{-x+b}{-x-b}$)=log2($\frac{x-b}{x+b}$)=-log2($\frac{x+b}{x-b}$)=-f(x),
故函数f(x)为奇函数,
(3)若f(x)≥1,则$\frac{x+b}{x-b}$≥2,
即$\frac{-x+3b}{x-b}$≥0,
当b<0时,不等式的解集为[3b,b),
当b>0时,不等式的解集为(b,3b]
点评 本题考查的知识点是对数函数的图象和性质,分类讨论思想,熟练掌握对数函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
12.若双曲线的顶点为椭圆x2+$\frac{y^2}{2}$=1长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程是$\frac{y^2}{2}-\frac{x^2}{2}=1$.
9.下列函数中,不是偶函数的是( )
| A. | f(x)=x3 | B. | f(x)=x2+1 | C. | $f(x)=\frac{1}{x^2}$ | D. | f(x)=|x| |
16.如图是偶函数y=f(x)的局部图象,根据图象所给信息,下列结论正确的是( )
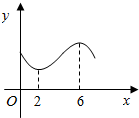

| A. | f(-2)-f(6)=0 | B. | f(-2)-f(6)<0 | C. | f(-2)+f(6)=0 | D. | f(-2)-f(6)>0 |
13.设P和Q是两个集合,定义集合P+Q={x∈P或x∈Q且∉P∩Q},若P={x|x2-3x-4≤0},Q={x|y=log2(x2-2x-15)},那么P+Q等于( )
| A. | [-1,4] | B. | (-∞,-1]∪[4,+∞) | C. | (-3,5) | D. | (-∞,-3)∪[-1,4]∪(5,+∞) |