题目内容
已知y=f(x)是定义在R上的函数,且对任意x∈R,都有f(x+2)=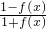 ,又f(1)=
,又f(1)= ,f(2)=
,f(2)= ,则f(2010)等于
,则f(2010)等于
- A.

- B.

- C.

- D.

C
分析:直接利用条件求出前几项,发现其规律为偶数中4的倍数对应的为 ,不是4的倍数对应的值为
,不是4的倍数对应的值为 ,即可求得结论.
,即可求得结论.
解答:都有f(x+2)=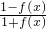 ,又f(1)=
,又f(1)= ,f(2)=
,f(2)= ,
,
f(4)= ,f(6)=
,f(6)= ,(8)=
,(8)= ,f(10)=
,f(10)= …
…
其规律为偶数中4的倍数对应的为 ,不是4的倍数对应的值为
,不是4的倍数对应的值为 ,
,
而2010不能被4整除,故f(2010)= .
.
故选C.
点评:本题是对抽象函数周期性的考查.抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.另外,发掘函数值出现的规律也应有做够的意识.
分析:直接利用条件求出前几项,发现其规律为偶数中4的倍数对应的为
 ,不是4的倍数对应的值为
,不是4的倍数对应的值为 ,即可求得结论.
,即可求得结论.解答:都有f(x+2)=
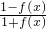 ,又f(1)=
,又f(1)= ,f(2)=
,f(2)= ,
,f(4)=
 ,f(6)=
,f(6)= ,(8)=
,(8)= ,f(10)=
,f(10)= …
…其规律为偶数中4的倍数对应的为
 ,不是4的倍数对应的值为
,不是4的倍数对应的值为 ,
,而2010不能被4整除,故f(2010)=
 .
.故选C.
点评:本题是对抽象函数周期性的考查.抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.另外,发掘函数值出现的规律也应有做够的意识.

练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+ 已知函数f(x)=2x+
已知函数f(x)=2x+