题目内容
椭圆的中心是原点O,短轴长为2| 3 |
| AO |
(Ⅰ)求椭圆的方程;
(Ⅱ)若PF⊥QF,求直线PQ的方程;
(Ⅲ)设
| AQ |
| AP |
| FQ′ |
| FP |
分析:(I)由题意可得2b=2
,
-c=3c结合a2=b2+c2可求a,b,c,进而求椭圆的方程
(II)可先设PQ:y=k(x+4),P(x1,y1),Q(x2,y2),F(-1,0)由PF⊥QF可得(x1+1)(x2+1)+y1y2=0
故需要联立方程
,可得(3+4k2)x2+32k2x+64k2-12=0,进而可得x1x2=
,x1+x2=-
,代入可求
(III)要证
=-λ
,只要证明P、F、Q三点共线且点F在线段PQ′上,
与
反向即可
| 3 |
| a2 |
| c |
(II)可先设PQ:y=k(x+4),P(x1,y1),Q(x2,y2),F(-1,0)由PF⊥QF可得(x1+1)(x2+1)+y1y2=0
故需要联立方程
|
| 64k2-12 |
| 3+4k2 |
| 32k2 |
| 3+4k2 |
(III)要证
| FQ′ |
| FP |
| FQ′ |
| FP |
解答:解:(I)由题意可得2b=2
,
-c=3c
∵a2=b2+c2∴a=2,b=
∴椭圆的方程为
+
=1
(II)设PQ:y=k(x+4),P(x1,y1),Q(x2,y2),F(-1,0)
∵PF⊥QF∴(x1+1)(x2+1)+y1y2=0∴(x1+1)(x2+1)+k2 (x1+4)(x2+4)=0
∴(1+k2)x1x2+(1+4k2)(x1+x2)+(1+16k2)=0
联立
,消去y得(3+4k2)x2+32k2x+64k2-12=0
∴x1x2=
,x1+x2=-
代入化简得8k2=1∴k=±
.
∴直线PQ的方程为y=
(x+4)或y=-
(x+4).
(III)如图所示,
=
=λ
又|QN|=2|QF|,|PM|=2|PF|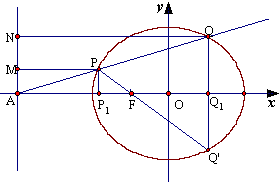 ∴
∴
=λ
又|FQ′|=|FQ|∴
=λ
再
=
=λ∴
=
=λ
又∠PP1F=∠Q′Q1F=90°
∴P、F、Q三点共线且点F在线段PQ′上,
与
反向.
∴
=-λ
.
| 3 |
| a2 |
| c |
∵a2=b2+c2∴a=2,b=
| 3 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)设PQ:y=k(x+4),P(x1,y1),Q(x2,y2),F(-1,0)
∵PF⊥QF∴(x1+1)(x2+1)+y1y2=0∴(x1+1)(x2+1)+k2 (x1+4)(x2+4)=0
∴(1+k2)x1x2+(1+4k2)(x1+x2)+(1+16k2)=0
联立
|
∴x1x2=
| 64k2-12 |
| 3+4k2 |
| 32k2 |
| 3+4k2 |
代入化简得8k2=1∴k=±
| ||
| 4 |
∴直线PQ的方程为y=
| ||
| 4 |
| ||
| 4 |
(III)如图所示,
| |QN| |
| |PM| |
| |AQ| |
| |AP| |
又|QN|=2|QF|,|PM|=2|PF|
 ∴
∴| |QF| |
| |PF| |
又|FQ′|=|FQ|∴
| |FQ′| |
| |PF| |
再
| |QQ1| |
| |PP1| |
| |AQ| |
| |AP| |
| |Q′Q1| |
| |PP1| |
| |FQ′| |
| |PF| |
又∠PP1F=∠Q′Q1F=90°
∴P、F、Q三点共线且点F在线段PQ′上,
| FQ′ |
| FP |
∴
| FQ′ |
| FP |
点评:本题主要考查了椭圆的性质在椭圆的方程求解中的应用,直线与椭圆的位置关系的应用,属于综合性试题,考查了考试的逻辑推理与运算的能力

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)( )的准线
)的准线 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 .
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 . ,求直线PQ的方程;
,求直线PQ的方程; (
( ),过点P且平行于准线
),过点P且平行于准线 .
.