题目内容
在R上定义运算 :x
:x y=x(1-y) 若不等式(x-a)
y=x(1-y) 若不等式(x-a) (x+a)<1对任意实数x成立.则( )
(x+a)<1对任意实数x成立.则( )
A. B.
B. C.
C. D.
D.
【答案】
C
【解析】
试题分析:结合新定义,在R上定义运算 :x
:x y=x(1-y) ,那么可知不等式(x-a)
y=x(1-y) ,那么可知不等式(x-a) (x+a)<1,等价于(x-a)
(x+a)<1,等价于(x-a)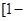 (x+a)]<1恒成立,对于任意的实数x,那么可知得到为
(x+a)]<1恒成立,对于任意的实数x,那么可知得到为 恒成立,故可知开口向上,判别式小于零即可,可知为
恒成立,故可知开口向上,判别式小于零即可,可知为 ,故选C.
,故选C.
考点:本试题考查了不等式的运用。
点评:对于不等式的恒成立问题,一般要转换为分离参数的思想来求解参数的取值范围即可,属于基础题。

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 :x
:x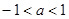 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.