Question

【题目】如图所示，正方体ABCD﹣A1B1C1D1的棱长为1，BD∩AC=0，M是线段D1O上的动点，过点M做平面ACD1的垂线交平面A1B1C1D1于点N，则点N到点A距离的最小值为（ ）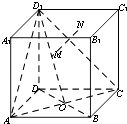

A.
B.
C.
D.1

Answer 1

【答案】B
【解析】解：∵平面ACD1⊥平面BDD1B1 ， 又MN⊥平面ACD1 ，
∴MN平面BDD1B1 ， ∴N∈B1D1
过N作NG⊥A1B1 ， 交A1B1于G，将平面A1B1C1D1展开，如图：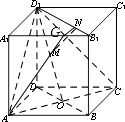

设NG=x，（0≤x≤1），
∴AN= = = ≥ ，
当x= 时最小．
故选B．
【考点精析】根据题目的已知条件，利用棱柱的结构特征的相关知识可以得到问题的答案，需要掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形．