题目内容
(本小题满分12分)
数列 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意 ,总有
,总有 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 设正数数列 满足
满足 ,求数列
,求数列 中的最大项;
中的最大项;
【答案】
(1) 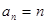
(2) 数列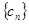 中的最大项为
中的最大项为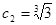
【解析】解:(1)由已知:对于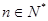 ,总有
,总有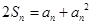 ①成立
①成立
∴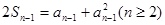 ②
②
① ②得
②得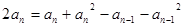
∴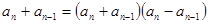 ∵
∵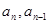 均为正数,∴
均为正数,∴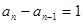
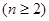
∴数列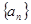 是公差为1的等差数列 又
是公差为1的等差数列 又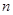 =1时,
=1时,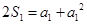 , 解得
, 解得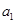 =1.
=1.
∴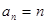 .
………………………………………6分
.
………………………………………6分
(2)(解法一)由已知 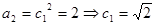 ,
,
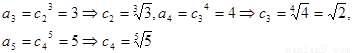
易得 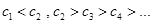 猜想
猜想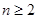 时,
时,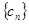 是递减数列............8分
是递减数列............8分
令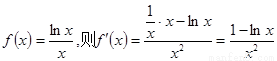
∵当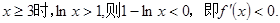
∴在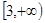 内
内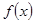 为单调递减函数.....................................10分
为单调递减函数.....................................10分
由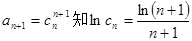 .
.
∴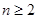 时,
时, 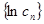 是递减数列.即
是递减数列.即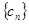 是递减数列.
是递减数列.
又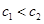 , ∴数列
, ∴数列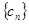 中的最大项为
中的最大项为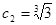 . ………………………………12分
. ………………………………12分

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目