题目内容
【题目】过点![]() 作直线
作直线![]() 分别交
分别交![]() 轴的正半轴于
轴的正半轴于![]() 两点.
两点.
(Ⅰ)当![]() 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线![]() 的方程;
的方程;
(Ⅱ)当![]() 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线![]() 的方程;
的方程;
(Ⅲ)当![]() 取最小值时,求出最小值及直线
取最小值时,求出最小值及直线![]() 的方程.
的方程.
【答案】(Ⅰ)答案见解析;(Ⅱ)答案见解析;(Ⅲ)答案见解析.
【解析】试题分析:(Ⅰ)设![]() . 设直线方程为
. 设直线方程为![]() ,代入
,代入![]() 得
得![]() ,
,
由假能诺丁山可得![]() ,此时
,此时![]() ,而斜率
,而斜率![]() .,由点斜式可得直线方程
.,由点斜式可得直线方程
(Ⅱ)![]() 由基本不等式可求
由基本不等式可求![]() 的最小值,此时
的最小值,此时![]() ,可求斜率
,可求斜率![]() ,则直线方程可求
,则直线方程可求
(Ⅲ)设直线![]() ,则
,则![]() .
.
则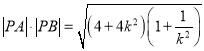 =
= ,
,
当且仅当![]() ,时,
,时, ![]() 取最小值,又∵
取最小值,又∵![]() ,可得
,可得![]() ,则直线方程可求
,则直线方程可求
试题解析:设![]() .
.
(Ⅰ)设直线方程为![]() ,代入
,代入![]() 得
得![]() ,
,
得![]() ,从而
,从而![]() ,此时
,此时![]() ,
, ![]() .
.
∴方程为![]() .
.
(Ⅱ)![]()
![]() ,
,
此时![]() ,
, ![]() .
.
∴方程为![]() .
.
(Ⅲ)设直线![]() ,分别令
,分别令![]() ,得
,得![]() .
.
则 =
=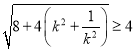 ,
,
当且仅当![]() ,即
,即![]() 时,
时, ![]() 取最小值,又∵
取最小值,又∵![]() ,
,
∴![]() ,这时
,这时![]() 的方程为
的方程为![]() .
.
【点击】本题考查三角形的面积公式、两点间的距离公式及基本不等式的应用,解题时要注意应用基本不等式时需满足的条件.

练习册系列答案
相关题目