题目内容
已知数列![]() 是正项等比数列,满足
是正项等比数列,满足
![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
解:(1)数列{an}的前n项和![]() ,
,
![]()
又![]() ,
,
![]()
![]() 是正项等比数列,
是正项等比数列,
![]() ,
,
公比![]() ,
,
数列![]()
(2)解法一:![]() ,
,
由![]()
![]() ,
,
当![]() ,
,
又![]()
故存在正整数M,使得对一切![]() M的最小值为2
M的最小值为2
(2)解法二:![]() ,
,
令![]() ,
,
由![]() ,
,
函数![]()
对于![]()
故存在正整数M,使得对一切![]() 恒成立,M的最小值为2。
恒成立,M的最小值为2。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
已知数列 是正项等比数列,
是正项等比数列,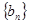 是等差数列,且
是等差数列,且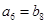 ,则
,则
A. | B. |
C.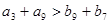 | D.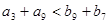 |
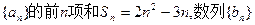 是正项等比数列,满足
是正项等比数列,满足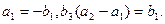
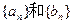 的通项公式;
的通项公式;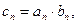 是否存在正整数
是否存在正整数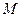 ,使得对一切
,使得对一切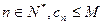 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。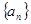 是正项等比数列,
是正项等比数列,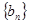 是等差数列,且
是等差数列,且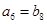 ,则
,则 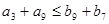 (B)
(B)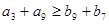
 (D)
(D)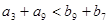
 是正项等比数列,满足
是正项等比数列,满足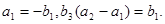
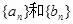 的通项公式;
的通项公式;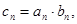 是否存在正整数
是否存在正整数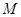 ,使得对一切
,使得对一切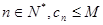 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。