题目内容
已知函数 的定义域为R,当
的定义域为R,当 时,
时,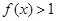 ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列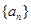 满足
满足 ,且
,且
( N*),则
N*),则 的值为( )
的值为( )
| A.4024 | B.4023 | C.4022 | D.4021 |
B
解析试题分析:根据题意, 不妨构造函数f(x)=
不妨构造函数f(x)=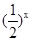
则 =1,∵
=1,∵ (n∈N*),
(n∈N*),
∴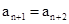 ,数列{an}是以1为首项,以2为公差的等差数列
,数列{an}是以1为首项,以2为公差的等差数列
∴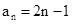 ,
, =4023
=4023
故选B。
考点:本题主要考查抽象函数的概念,等差数列的通项公式。
点评:典型题,本题看似复杂,但作为选择题,其解法则具有灵活性,本解法通过构造“符合题意”的函数,将抽象问题具体化。

练习册系列答案
相关题目
定义在 上的函数
上的函数 满足
满足 .当
.当 时,
时,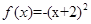 ,当
,当 时,
时, 。则
。则 ( )
( )
| A.335 | B.338 | C.1678 | D.2012 |
方程lgx+x=3的解所在区间为
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,+∞) |
函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
函数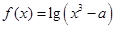 的定义域为[-1,1],且存在零点,则实数
的定义域为[-1,1],且存在零点,则实数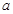 的取值范围是( )
的取值范围是( )
A.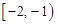 | B.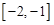 | C.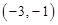 | D.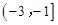 |
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则 ,在
,在 上所有零点之和为( )
上所有零点之和为( )
| A.7 | B.8 | C.9 | D.10 |
函数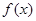 的定义域为
的定义域为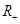 ,若
,若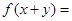
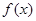
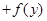 ,
,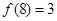 ,则
,则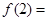 ( )
( )
A.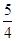 | B.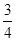 | C. | D.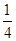 |
对于正实数 ,记
,记 为满足下述条件的函数
为满足下述条件的函数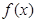 构成的集合:
构成的集合: 且
且 ,有
,有 .下列结论中正确的是
.下列结论中正确的是
A.若 ,则 ,则 |
B.若 且 且 ,则 ,则 |
C.若 ,则 ,则 |
D.若 且 且 ,则 ,则 |
若函数 的定义域为
的定义域为 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
A. | B.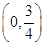 | C.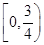 | D.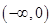 |