题目内容
已知 是两个不同的平面,
是两个不同的平面, 是两条不重合的直线,则下列命题中正确的是( )
是两条不重合的直线,则下列命题中正确的是( )
A. 若 ,则
,则 B. 若
B. 若 ,则
,则
C. 若 ,则
,则 D. 若
D. 若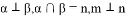 ,则
,则
练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
题目内容
已知 是两个不同的平面,
是两个不同的平面, 是两条不重合的直线,则下列命题中正确的是( )
是两条不重合的直线,则下列命题中正确的是( )
A. 若 ,则
,则 B. 若
B. 若 ,则
,则
C. 若 ,则
,则 D. 若
D. 若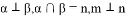 ,则
,则
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案