��Ŀ����
(������)
��1����ԲO��һ��P��������Բ���ڵ�A��MΪPA�е㣬��M�����߽�Բ��B��C���㣮
��֤����MCP=��MPB��
��2����ƽ��ֱ������ϵxOy�У���֪�ı���ABCD���ĸ�����A��0��1����B��2��1����C��2��3����D��0��2���������� ��ʾ�ı任���ú��ı���ABCD��Ϊ�ı���A1B1C1D1���ʣ��ı���ABCD���ı���A1B1C1D1������Ƿ���ȣ���֤����Ľ��ۣ�
��ʾ�ı任���ú��ı���ABCD��Ϊ�ı���A1B1C1D1���ʣ��ı���ABCD���ı���A1B1C1D1������Ƿ���ȣ���֤����Ľ��ۣ�
��3����֪A�����ߦ�=12sin���ϵĶ��㣬B������ �ϵĶ��㣬����AB�����ֵ��
�ϵĶ��㣬����AB�����ֵ��
��4����p�ǡ�ABC�ڵ�һ�㣬x��y��z��p������a��b��c�ľ��룬R�ǡ�ABC���Բ�İ뾶��֤�� ��
��
��1����ԲO��һ��P��������Բ���ڵ�A��MΪPA�е㣬��M�����߽�Բ��B��C���㣮
��֤����MCP=��MPB��
��2����ƽ��ֱ������ϵxOy�У���֪�ı���ABCD���ĸ�����A��0��1����B��2��1����C��2��3����D��0��2����������
 ��ʾ�ı任���ú��ı���ABCD��Ϊ�ı���A1B1C1D1���ʣ��ı���ABCD���ı���A1B1C1D1������Ƿ���ȣ���֤����Ľ��ۣ�
��ʾ�ı任���ú��ı���ABCD��Ϊ�ı���A1B1C1D1���ʣ��ı���ABCD���ı���A1B1C1D1������Ƿ���ȣ���֤����Ľ��ۣ���3����֪A�����ߦ�=12sin���ϵĶ��㣬B������
 �ϵĶ��㣬����AB�����ֵ��
�ϵĶ��㣬����AB�����ֵ����4����p�ǡ�ABC�ڵ�һ�㣬x��y��z��p������a��b��c�ľ��룬R�ǡ�ABC���Բ�İ뾶��֤��
 ��
��
��1��֤������AM��Բ�ڵ�A��
��AM2=MB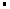 MC
MC
�֡�MΪPA�е㣬AM=MP��
��MP2=MB MC��
MC��
��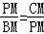
�ߡ�BMP=��PMC��
���BMP�ס�PMC��
���MCP=��MPB��
��2���ĸ�����A��0��1����B��2��1����C��2��3����D��0��2����
������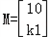 ��ʾ�ı任���ú�
��ʾ�ı任���ú�
�ı���ABCD��Ϊ�ı���A1B1C1D1��������Ϊ
A1��0��1����B1��2��2k+1����C1��2��2k+3����D1��0��2����
�ı���A1B1C1D1��Ϊ���Σ����ϡ��µ��߶����䣬�������ȣ�
��3�����ߦ�=12sin�Ȼ�Ϊֱ�����귽��Ϊ x2+��y��6��2=36��
��ʾ�ԣ�0��6��ΪԲ�ģ���6Ϊ�뾶��Բ��
����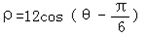 ��Ϊֱ�����귽��Ϊ
��Ϊֱ�����귽��Ϊ
x2+y2=6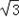 x+6y���� ��x��3
x+6y���� ��x��3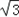 ��2+��y��3��2=36��
��2+��y��3��2=36��
��ʾ�ԣ�3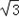 ��3 ��ΪԲ�ģ���6Ϊ�뾶��Բ��
��3 ��ΪԲ�ģ���6Ϊ�뾶��Բ��
��Բ��Բ�ľ��ƽ��Ϊ ��0��3 ��2+��6��3��2 =36��
��2+��6��3��2 =36��
����Բ�ཻ���߶�AB�������ֵΪ6+r+r'=18��
��4������P�������ε��������㣬�ֳɵ�����С����������ĺ͵��ڴ������Σ�
�� ��ax+by+cz��=S��
��ax+by+cz��=S��
��ax+by+cz=2S=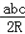
��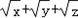 =
=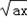 ��
��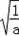 +
+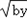 ��
��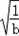 +
+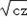 ��
��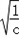
��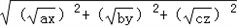 ��[
��[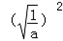 +
+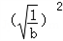 +
+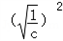 ]
]
=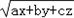 ����
����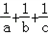 ��=
��=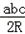 ��
��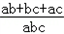
=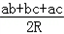 ��
��
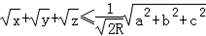
��AM2=MB
 MC
MC�֡�MΪPA�е㣬AM=MP��
��MP2=MB
 MC��
MC����
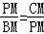
�ߡ�BMP=��PMC��
���BMP�ס�PMC��
���MCP=��MPB��
��2���ĸ�����A��0��1����B��2��1����C��2��3����D��0��2����
������
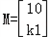 ��ʾ�ı任���ú�
��ʾ�ı任���ú��ı���ABCD��Ϊ�ı���A1B1C1D1��������Ϊ
A1��0��1����B1��2��2k+1����C1��2��2k+3����D1��0��2����
�ı���A1B1C1D1��Ϊ���Σ����ϡ��µ��߶����䣬�������ȣ�
��3�����ߦ�=12sin�Ȼ�Ϊֱ�����귽��Ϊ x2+��y��6��2=36��
��ʾ�ԣ�0��6��ΪԲ�ģ���6Ϊ�뾶��Բ��
����
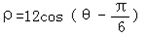 ��Ϊֱ�����귽��Ϊ
��Ϊֱ�����귽��Ϊx2+y2=6
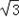 x+6y���� ��x��3
x+6y���� ��x��3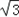 ��2+��y��3��2=36��
��2+��y��3��2=36����ʾ�ԣ�3
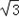 ��3 ��ΪԲ�ģ���6Ϊ�뾶��Բ��
��3 ��ΪԲ�ģ���6Ϊ�뾶��Բ����Բ��Բ�ľ��ƽ��Ϊ ��0��3
 ��2+��6��3��2 =36��
��2+��6��3��2 =36������Բ�ཻ���߶�AB�������ֵΪ6+r+r'=18��
��4������P�������ε��������㣬�ֳɵ�����С����������ĺ͵��ڴ������Σ�
��
 ��ax+by+cz��=S��
��ax+by+cz��=S����ax+by+cz=2S=
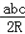
��
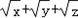 =
=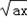 ��
��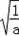 +
+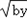 ��
��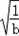 +
+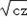 ��
��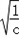
��
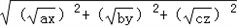 ��[
��[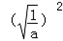 +
+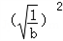 +
+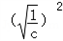 ]
]=
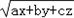 ����
����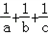 ��=
��=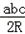 ��
��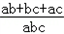
=
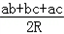 ��
��
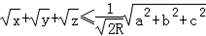

��ϰ��ϵ�д�
�����Ŀ