题目内容
曲线y=sinx+cosx在点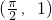
处的切线斜率为________．
-1
分析：求出曲线方程的导函数，把切点的横坐标代入导函数中即可求出切线方程的斜率．
解答：求导得：y′=cosx-sinx，
把x=
代入导函数得：
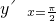=0-1=-1，
则所求切线的斜率为-1．
故答案为：-1
点评：此题考查学生会利用导数求曲线上过某点切线方程的斜率，是一道基础题．
分析：求出曲线方程的导函数，把切点的横坐标代入导函数中即可求出切线方程的斜率．
解答：求导得：y′=cosx-sinx，
把x=
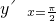代入导函数得：=0-1=-1，则所求切线的斜率为-1．
故答案为：-1
点评：此题考查学生会利用导数求曲线上过某点切线方程的斜率，是一道基础题．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
当点P在曲线y=sinx（x∈（0，π））上移动时，曲线在P处切线的倾斜角的取值范围是（ ）
A、[0，
| ||||
B、(-
| ||||
C、(
| ||||
D、[0，
|
M，N是曲线y=πsinx与曲线y=πcosx的两个不同的交点，则|MN|的最小值为（ ）
| A、π | ||
B、
| ||
C、
| ||
| D、2π |
在利用随机模拟求图（其中矩形OABC的长为π，宽为2）中阴影（由曲线y=sinx（0≤x≤π）与x轴围成）面积的过程中，随机产生N1组随机数据（xi，yi），（i=1，2，3∧N1），其对应的点都落在矩形OABC区域内，其中有N2个点落在阴影区域内，现已知N1=10，据此估计N2的值为（ ）说明：[x]表示实数x的整数部分．
如图，圆O：x2+y2=