题目内容

M，N是曲线y=πsinx与曲线y=πcosx的两个不同的交点，则|MN|的最小值为（　　）
A、π
B、
2
π
C、
3
π
D、2π
分析：|MN|的最小值即一个周期内两个交点的距离；列出方程求出两个交点坐标，据两点的距离公式求出|MN|的最小值．
解答：解：要求|MN|的最小值在，只要在一个周期内解即可
∵πsinx=πcosx 解得x=
π
4
或x=
5π
4

得到两个点为（，
π
4
，
2
π
2
）和（
5π
4
，-
2
π
2
）
得到|MN|=
(
5π
4
-
π
4
)2+(-
2
π
2
-
2
π
2
 )2
=
3
π
故选C
点评：本题考查等价转化的数学思想方法、两点的距离公式．
练习册系列答案
相关题目
已知圆C1：（x+1）2+y2=8，点C2（1，0），点Q在圆C1上运动，QC2的垂直平分线交QC1于点P．
（Ⅰ） 求动点P的轨迹W的方程；
（Ⅱ） 设M，N是曲线W上的两个不同点，且点M在第一象限，点N在第三象限，若
OM
+2
ON
=2
OC1
，O为坐标原点，求直线MN的斜率k；
（Ⅲ）过点S(0，-
1
3
)且斜率为k的动直线l交曲线W于A，B两点，在y轴上是否存在定点D，使以AB为直径的圆恒过这个点？若存在，求出D的坐标，若不存在，说明理由．
已知A、B分别是x轴和y轴上的两个动点，满足|AB|=2，点P在线段AB上且
AP
=2
PB
，设点P的轨迹方程为C．
（Ⅰ）求曲线C的方程；
（Ⅱ）若点M、N是曲线C上关于原点对称的两个动点，点Q的坐标为(
3
2
，3)，求△QMN的面积S的最大值．
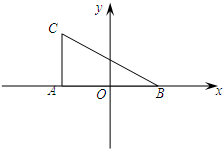精英家教网如图，在Rt△ABC中，∠CAB=90°，|AB|=2，|AC|=
3
2
，点A，B关于y轴对称．一曲线E过C点，动点P在曲线E上运动，且保持|PA|+|PB|的值不变．
（1）求曲线E的方程；
（2）已知点S(0，-
3
)，T(0，
3
)，求∠SPT的最小值；
（3）若点F(1，
3
2
)是曲线E上的一点，设M，N是曲线E上不同的两点，直线FM和FN的倾斜角互补，试判断直线MN的斜率是否为定值，如果是，求出这个定值；如果不是，请说明理由．
已知A、B分别是x轴和y轴上的两个动点，满足|AB|=2，点P在线段AB上且
AP
=2
PB
，设点P的轨迹方程为C．
（Ⅰ）求曲线C的方程；
（Ⅱ）若点M、N是曲线C上关于原点对称的两个动点，点Q的坐标为(
3
2
，3)，求△QMN的面积S的最大值．
已知动点A、B分别在x轴、y轴上,且满足|AB|=2,点P在线段AB上,且=2.设点P的轨迹方程为C.

(1)求点P的轨迹方程C;

(2)若点M、N是曲线C上关于原点对称的两个动点,点Q的坐标为(,3),求△QMN的面积S的最大值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网