题目内容
下列说法中,正确的是( )①对于定义域为R的函数f(x),若函数f(x)满足f(x+1)=f(1-x),则函数f(x)的图象关于x=1对称;
②当a>1时,任取x∈R都有ax>a-x;
③“a=1”是“函数f(x)=lg(ax+1)在(0,+∞)上单调递增”的充分必要条件;
④设a∈{-1,1,
 ,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3;
,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3;⑤已知a是函数f(x)=2x-log0.5x的零点,若0<x<a,则f(x)<0.
A.①④
B.①④⑤
C.②③④
D.①⑤
【答案】分析:对①根据条件f(x+1)=f(1-x)与f(x)=f(2-x)等同,利用点关于直线的对称点在函数图象上来判断函数图象的对称性;
对②x 与-x的大小不确定,可判断;根据函数f(x)=lg(ax+1)在(0,+∞)上单调递增的条件,可判断③是否正确;
对④根据幂函数的性质可求出符合条件的指数;
对⑤根据函数y=2x,y=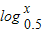 的单调性确定f(x)=2x-log0.5x的单调性,来判断⑤是否正确.
的单调性确定f(x)=2x-log0.5x的单调性,来判断⑤是否正确.
解答:解:∵f(x)满足f(x+1)=f(1-x),∴f(a)=f(2-a),设M(a、b)是函数上的任一点,M关于x=1的对称点N(2-a,b)也在函数图象上,∴f(x)的图象关于x=1直线对称,①正确;
∵a>1,y=ax为增函数,x与-x大小不定,∴②不正确;
∵a>0 时函数f(x)=lg(ax+1)在(0,+∞)上单调递增,∴是充分不必要条件,故③不正确;
∵a=-1时定义域为{x|x≠0,x∈R},a= 时定义域是x≥0,a=1或3时,定义域为R且该函数为奇函数,故④正确;
时定义域是x≥0,a=1或3时,定义域为R且该函数为奇函数,故④正确;
∵f(a)=2a-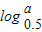 =0,∵y=2x为增函数,y=
=0,∵y=2x为增函数,y=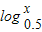 为减函数,∴f(x)=2x-log0.5x为增函数,∴0<x<a,f(x)<f(a)=0,故⑤正确;
为减函数,∴f(x)=2x-log0.5x为增函数,∴0<x<a,f(x)<f(a)=0,故⑤正确;
故答案是①④⑤
点评:本题考查了幂函数、指数函数、对数函数的图象、性质及应用;特别注意可用点关于直线的对称点在函数图象上来判断和证明函数图象的对称性.这是证明函数图象对称性的常用方法.
对②x 与-x的大小不确定,可判断;根据函数f(x)=lg(ax+1)在(0,+∞)上单调递增的条件,可判断③是否正确;
对④根据幂函数的性质可求出符合条件的指数;
对⑤根据函数y=2x,y=
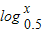 的单调性确定f(x)=2x-log0.5x的单调性,来判断⑤是否正确.
的单调性确定f(x)=2x-log0.5x的单调性,来判断⑤是否正确.解答:解:∵f(x)满足f(x+1)=f(1-x),∴f(a)=f(2-a),设M(a、b)是函数上的任一点,M关于x=1的对称点N(2-a,b)也在函数图象上,∴f(x)的图象关于x=1直线对称,①正确;
∵a>1,y=ax为增函数,x与-x大小不定,∴②不正确;
∵a>0 时函数f(x)=lg(ax+1)在(0,+∞)上单调递增,∴是充分不必要条件,故③不正确;
∵a=-1时定义域为{x|x≠0,x∈R},a=
 时定义域是x≥0,a=1或3时,定义域为R且该函数为奇函数,故④正确;
时定义域是x≥0,a=1或3时,定义域为R且该函数为奇函数,故④正确;∵f(a)=2a-
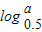 =0,∵y=2x为增函数,y=
=0,∵y=2x为增函数,y=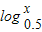 为减函数,∴f(x)=2x-log0.5x为增函数,∴0<x<a,f(x)<f(a)=0,故⑤正确;
为减函数,∴f(x)=2x-log0.5x为增函数,∴0<x<a,f(x)<f(a)=0,故⑤正确;故答案是①④⑤
点评:本题考查了幂函数、指数函数、对数函数的图象、性质及应用;特别注意可用点关于直线的对称点在函数图象上来判断和证明函数图象的对称性.这是证明函数图象对称性的常用方法.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目