题目内容
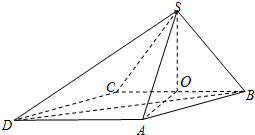 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2| 2 |
| 3 |
(1)证明:SA⊥BC;
(2)求直线SD与平面SAB所成角的大小;
(3)求二面角D-SA-B的大小.
分析:(1)根据条件中所给的两两垂直的三条直线建立坐标系,写出要用的点的坐标,写出
,
的坐标,根据求出两个向量的数量积为0,得到两个向量垂直.
(2)求线面角,写出线对应的向量,求出一条直线与平面垂直,这是平面的一个法向量,根据两个向量的夹角做出线与平面所成的角的正弦.
(3)要求两个平面的二面角,需要做出两个平面的法向量,根据上一问知道
为平面SAB的法向量,只要求出面SDB的一个法向量,利用两个法向量的夹角的余弦值,得到两个向量的夹角.
| SA |
| CB |
(2)求线面角,写出线对应的向量,求出一条直线与平面垂直,这是平面的一个法向量,根据两个向量的夹角做出线与平面所成的角的正弦.
(3)要求两个平面的二面角,需要做出两个平面的法向量,根据上一问知道
| OG |
解答: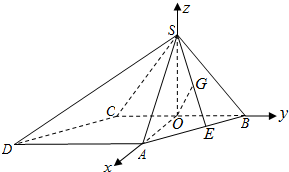 解:(1)作SO⊥BC,垂足为O,连接AO,由侧面SBC⊥底面ABCD,得SO⊥平面ABCD.
解:(1)作SO⊥BC,垂足为O,连接AO,由侧面SBC⊥底面ABCD,得SO⊥平面ABCD.
因为SA=SB,所以AO=BO.
又∠ABC=45°,△AOB为等腰直角三角形,AO⊥OB
如图,以O为坐标原点,OA为x轴正向,建立直角坐标系O-xyz
A(
,0,0),B(0,
,0),C(0,-
,0),S(0,0,1),
=(
,0,-1),
=(0,2
,0),
•
=0,
所以SA⊥BC
(2)取AB中点E,E(
,
,0),
连接SE,取SE中点G,连接OG,G(
,
,
).
=(
,
,
),
=(
,
,1),
=(-
,
,0).
•
=0,
•
=0,
OG与平面SAB内两条相交直线SE,AB垂直.
∴OG⊥平面SAB,
与
的夹角记为α,SD与平面SAB所成的角记为β,则α与β互余
D(
,2
,0),
=(-
,2
,1).
cosα=
=
,
∴sinβ=
,
(3)由上知
为平面SAB的法向量,
=(
,
)
易得D(
,-2
,0)
=(0,2
,0),
=(
,0,-1)
同理可求得平面SDA的一个法向量为
=(1,0,
)
∴cosθ=
=
由题知所求二面角为钝二面角,故二面角D-SA-B的大小为150°.
 解:(1)作SO⊥BC,垂足为O,连接AO,由侧面SBC⊥底面ABCD,得SO⊥平面ABCD.
解:(1)作SO⊥BC,垂足为O,连接AO,由侧面SBC⊥底面ABCD,得SO⊥平面ABCD. 因为SA=SB,所以AO=BO.
又∠ABC=45°,△AOB为等腰直角三角形,AO⊥OB
如图,以O为坐标原点,OA为x轴正向,建立直角坐标系O-xyz
A(
| 2 |
| 2 |
| 2 |
| SA |
| 2 |
| CB |
| 2 |
| SA |
| CB |
所以SA⊥BC
(2)取AB中点E,E(
| ||
| 2 |
| ||
| 2 |
连接SE,取SE中点G,连接OG,G(
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
. |
| OG |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
. |
| SE |
| ||
| 2 |
| ||
| 2 |
. |
| AB |
| 2 |
| 2 |
. |
| SE |
. |
| OG |
. |
| AB |
. |
| OG |
OG与平面SAB内两条相交直线SE,AB垂直.
∴OG⊥平面SAB,
. |
| OG |
. |
| DS |
D(
| 2 |
| 2 |
. |
| DS |
| 2 |
| 2 |
cosα=
| ||||
|
|
| ||
| 11 |
∴sinβ=
| ||
| 11 |
(3)由上知
| OG |
| OG |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
易得D(
| 2 |
| 2 |
| DA |
| 2 |
| SA |
| 2 |
同理可求得平面SDA的一个法向量为
| m |
| 2 |
∴cosθ=
| ||||
|
|
| ||
| 2 |
由题知所求二面角为钝二面角,故二面角D-SA-B的大小为150°.
点评:本题考查利用空间向量解决立体几何问题,解题的关键是建立坐标系,写出要用的点的坐标,进而写出向量的坐标,然后进行向量的有关运算.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
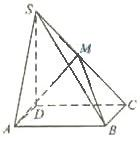 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=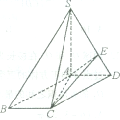 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥平面ABCD,AB=2,AD=1,
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥平面ABCD,AB=2,AD=1,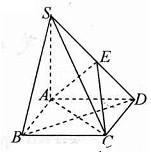 如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,SB=SD=2
如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,SB=SD=2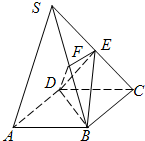 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,SD=AD,DF⊥SB垂足为F,E是SD的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,SD=AD,DF⊥SB垂足为F,E是SD的中点.