Question

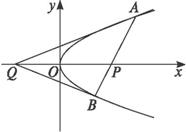
如图，已知动直线l经过点P（4，0），交抛物线y²=2ax（a＞0）于A，B两点，坐标原点O是PQ的中点，设直线AQ，BQ的斜率分别为k₁，k₂．
（1）证明：k₁+k₂=0；
（2）当a=2时，是否存在垂直于x轴的直线l′，被以AP为直径的圆截得的弦长为定值？若存在，请求出直线l′的方程；若不存在，请说明理由．

Answer 1

分析：（1）设直线l方程与抛物线方程联立可得：y²-2amy-8a=0，表示出直线AQ，BQ的斜率，利用韦达定理可证；
（2）假设存在这样的直线，记作l'：x=t．若要满足题意，只需r²-d²为常数即可．

解答：（1）证明：设直线l方程为x=my+4（m∈R），与抛物线方程联立可得：y²-2amy-8a=0，
再设点A(

y12

2a

，y1)，B(

y22

2a

，y2)，则y₁•y₂=-8a
所以k1=

y1

y12 2a +4

=

2ay1

y12+8a

=

2a• -8a y2

64a2 y22 +8a

=-

2ay2

y22+8a

=-k2，故k₁+k₂=0-----（7分）
（2）解：因为a=2，所以抛物线的方程为：y²=4x．
记线段AP中点即圆心为O′(

y12+16

8

，

y1

2

)，则圆的半径r=|O′P|=

( y12+16 8 -4)2+ y12 4

，
假设存在这样的直线，记作l'：x=t．若要满足题意，只需r²-d²为常数即可．--------（10分）
故r²-d²=(

y12+16

8

-4)2+

y12

4

-(t-

y12+16

8

)2=(

t

4

-

3

4

)y12-t2+4t
所以

t

4

=

3

4

，即t=3时，能保证为常数，故存在这样的直线l'：x=3满足题意．-----（15分）

点评：本题考查直线与抛物线的位置关系，考查韦达定理的运用，考查圆中弦长的计算，属于中档题．