题目内容
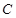 是以原点
是以原点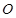 为中心,焦点在
为中心,焦点在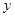 轴上的等轴双曲线在第一象限部分,曲线
轴上的等轴双曲线在第一象限部分,曲线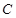 在点P处的切线分别交该双曲线的两条渐近线于
在点P处的切线分别交该双曲线的两条渐近线于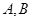 两点,则( )
两点,则( )A. | B. |
C. | D.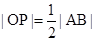 |
D
试题分析:设过点
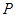 的切线为
的切线为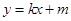 ,∴
,∴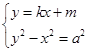 ,消
,消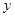 得:
得: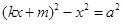 ,
,即
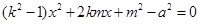 ,∴
,∴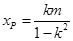 ,∴
,∴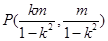 ,
,∵
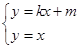 ,∴
,∴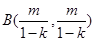 ,∵
,∵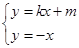 ,∴
,∴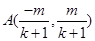 ,
,∴
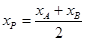 ,
,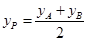 ,∴
,∴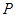 为
为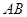 中点,
中点,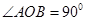 ,∴
,∴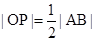 .
.
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
题目内容
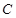 是以原点
是以原点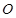 为中心,焦点在
为中心,焦点在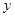 轴上的等轴双曲线在第一象限部分,曲线
轴上的等轴双曲线在第一象限部分,曲线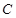 在点P处的切线分别交该双曲线的两条渐近线于
在点P处的切线分别交该双曲线的两条渐近线于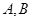 两点,则( )
两点,则( )A. | B. |
C. | D.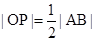 |
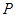 的切线为
的切线为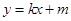 ,∴
,∴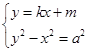 ,消
,消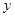 得:
得: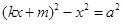 ,
,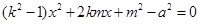 ,∴
,∴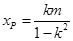 ,∴
,∴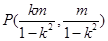 ,
,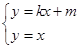 ,∴
,∴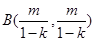 ,∵
,∵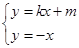 ,∴
,∴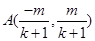 ,
,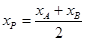 ,
,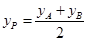 ,∴
,∴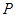 为
为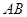 中点,
中点,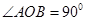 ,∴
,∴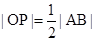 .
.
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案