题目内容
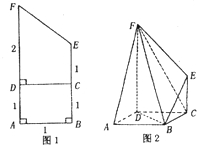 将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图2所示.
将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图2所示.(I)证明:直线BE∥平面ADF;
(II)求面FBE与面ABCD所成角的正切值.
分析:(I)取DF的中点为G,连接AG,EG,故GE
CD
AB,所以四边形ABEG为平行四边形,由此能够证明BE∥平面ADF.
(II)延长FE与DC交于H,连接BH,则BH是平面FBE与平面ABCD的交线,由∠FDC=
,且F-DC-A为直二面角,知FD⊥平面ABCD,故FD⊥BH,又CE
FD,所以在Rt△BCH中,∠CBH=
,由此能够求出平面FBE与平面ABCD所成角的正切值.
| ||
. |
| ||
. |
(II)延长FE与DC交于H,连接BH,则BH是平面FBE与平面ABCD的交线,由∠FDC=
| π |
| 2 |
| ||
. |
| 1 |
| 2 |
| π |
| 4 |
解答: (I)证明:取DF的中点为G,连接AG,EG,
(I)证明:取DF的中点为G,连接AG,EG,
∴GE
CD
AB,
∴四边形ABEG为平行四边形,
∴BE∥AG,
∵AG?平面ADF,BE?平面ADF,
∴BE∥平面ADF.
(II)解:延长FE与DC交于H,连接BH,
则BH是平面FBE与平面ABCD的交线,
∵∠FDC=
,且F-DC-A为直二面角,
∴FD⊥平面ABCD,
∴FD⊥BH,
又CE
FD,
∴DC=CH,
∴BC=CH,
∴在Rt△BCH中,∠CBH=
,
∴BH⊥BD,
∴BH⊥平面BDF.
∴∠DBF就是二面角F-BH-A的平面角,
在Rt△BDF中,∠BDF=
,DF=2,BD=
,
∴tan∠DBF=
=
=
,
∴平面FBE与平面ABCD所成角的正切值为
.
 (I)证明:取DF的中点为G,连接AG,EG,
(I)证明:取DF的中点为G,连接AG,EG,∴GE
| ||
. |
| ||
. |
∴四边形ABEG为平行四边形,
∴BE∥AG,
∵AG?平面ADF,BE?平面ADF,
∴BE∥平面ADF.
(II)解:延长FE与DC交于H,连接BH,
则BH是平面FBE与平面ABCD的交线,
∵∠FDC=
| π |
| 2 |
∴FD⊥平面ABCD,
∴FD⊥BH,
又CE
| ||
. |
| 1 |
| 2 |
∴DC=CH,
∴BC=CH,
∴在Rt△BCH中,∠CBH=
| π |
| 4 |
∴BH⊥BD,
∴BH⊥平面BDF.
∴∠DBF就是二面角F-BH-A的平面角,
在Rt△BDF中,∠BDF=
| π |
| 2 |
| 2 |
∴tan∠DBF=
| DF |
| BD |
| 2 | ||
|
| 2 |
∴平面FBE与平面ABCD所成角的正切值为
| 2 |
点评:本题考查直线与平面平行的证明,考查平面与平面所成角的正切值的求法,解题时要认真审题,仔细解答,注意合理地化立体问题为平面问题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
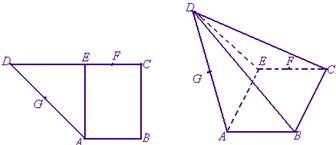
 如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,AB=2,E为AB的中点,将△ADE沿DE翻折至△A′DE,使二面角A′-DE-B为直二面角.
如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,AB=2,E为AB的中点,将△ADE沿DE翻折至△A′DE,使二面角A′-DE-B为直二面角. 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,