题目内容
(本小题共14分)已知![]() .
.
(1)求函数![]() 上的最小值;
上的最小值;
(2)已知![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:对一切![]() ,都有
,都有![]() 成立.
成立.
(本小题共14分)
解:(1)![]() , ………… 1分
, ………… 1分
当![]() 单调递减,当
单调递减,当![]() 单调递增 …2分
单调递增 …2分
①当![]() 时,
时,![]()
![]() ; ………………… 3分
; ………………… 3分
②当![]() ,即
,即![]() 时,
时,![]() 上单调递增,
上单调递增,
![]() ; ………………… 4分
; ………………… 4分
所以 ………………… 5分
………………… 5分
(2)在![]() 两边取对数得
两边取对数得![]() , ……………… 6分
, ……………… 6分
由于![]() ,所以
,所以![]() , ………………… 7分
, ………………… 7分
令![]() ,由(1)可知,当
,由(1)可知,当![]() 时,
时,![]() 8分
8分
所以![]() ,即
,即![]() 。 ………………… 9分
。 ………………… 9分
(3)问题等价于证明![]() , ………………… 10分
, ………………… 10分
由(1)可知![]() 的最小值是
的最小值是![]() ,当且仅当
,当且仅当![]() 时取到, 11分
时取到, 11分
设![]() ,则
,则![]() , ………………… 12分
, ………………… 12分
易知![]() ,当且仅当
,当且仅当![]() 时取到, ………………… 13分
时取到, ………………… 13分
从而对一切![]() ,都有
,都有![]() 成立 。 ………………… 14分
成立 。 ………………… 14分

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
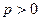 ,动点
,动点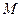 到定点
到定点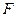
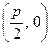 的距离比
的距离比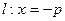 的距离小
的距离小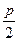 .
.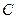 的方程;
的方程; 是轨迹
是轨迹 的两个不同点,
的两个不同点,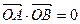 ,求
,求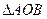 面积的最小值;
面积的最小值;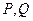 关于直线
关于直线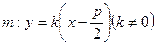 对称?若存在,求出直线
对称?若存在,求出直线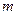 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.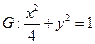 .过点(m,0)作圆
.过点(m,0)作圆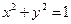 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.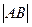 表示为m的函数,并求
表示为m的函数,并求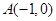 ,
,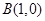 ,动点P满足
,动点P满足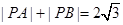 ,记动点P的轨迹为W.
,记动点P的轨迹为W.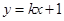 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点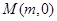 ,使得
,使得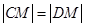 成立,求实数m的取值范围.
成立,求实数m的取值范围.