题目内容
下列关于函数y=sinx,x∈[-π,π]的单调性的叙述,正确的是( )
| A、在[-π,0]上是增函数,在[0,π]上是减函数 | ||||||||
B、在[-
| ||||||||
| C、在[0,π]上是增函数,在[-π,0]上是减函数 | ||||||||
D、在[
|
分析:根据正弦函数的图象与性质,我们根据正弦函数的单调性,我们易判断出函数y=sinx,x∈[-π,π]的单调性,比照题目中的四个答案后,即可得到结论.
解答:解:对于函数y=sinx,x∈[-π,π]
我们易得其在x=-
时,函数取最小值,当x=
时,函数取最大值,
故函数在[-
,
]上是增函数,在[-π,-
]及[
,π]上是减函数
故选B
我们易得其在x=-
| π |
| 2 |
| π |
| 2 |
故函数在[-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故选B
点评:本题考查的知识点是正弦函数的单调性,熟练掌握正弦函数的图象和性质是解答本题的关键,属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上是增函数,在[-π,-
上是增函数,在[-π,- ]及[
]及[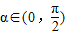 ,使
,使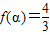 ;②存在
;②存在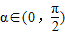 ,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点
,使f(x+α)=f(x+3α);③存在θ∈R使函数f(x+θ)的图象关于y轴对称;④函数f(x)的图象关于点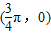 对称.
对称.