题目内容
已知函数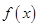 是奇函数,当
是奇函数,当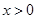 时,
时,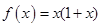 ;当
;当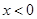 时,
时,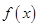 =
=
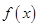 是奇函数,当
是奇函数,当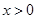 时,
时,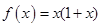 ;当
;当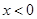 时,
时,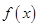 =
=A.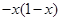 | B.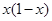 | C. | D.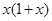 |
B
要求x<0时的解析式,先设x<0,则-x>0,因为已知x>0时函数的解析式,所以可求出f(-x),再根据函数的奇偶性来求f(x)与f(-x)之间的关系可求
解:设x<0,则-x>0,
∵当x>0时,f(x)=x(-x+1),
∴f(-x)=-x(x+1)
又∵f(x)是定义在R上的奇函数,
∴f(x)=-f(-x)=x(x+1)
故选B
解:设x<0,则-x>0,
∵当x>0时,f(x)=x(-x+1),
∴f(-x)=-x(x+1)
又∵f(x)是定义在R上的奇函数,
∴f(x)=-f(-x)=x(x+1)
故选B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
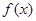 是定义在R上的奇函数,且
是定义在R上的奇函数,且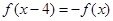 ,在[0,2]上
,在[0,2]上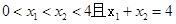 ,则
,则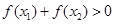 ;②若
;②若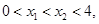 且
且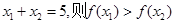 ③若方程
③若方程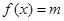 在[-8,8]内恰有四个不同的角
在[-8,8]内恰有四个不同的角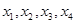 ,则
,则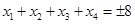 ,其中正确的有 ( )
,其中正确的有 ( )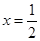
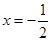
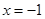
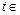 R,m,n都是不为1的正数,函数
R,m,n都是不为1的正数,函数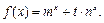
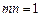 ,请判断函数
,请判断函数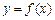 是否具有奇偶性. 如果具有,求出相
是否具有奇偶性. 如果具有,求出相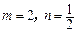 ,且
,且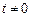 ,请判断函数
,请判断函数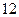 分)
分)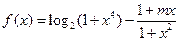
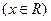 是偶函数.
是偶函数.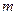 的值,并给出函数
的值,并给出函数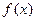 的单调区间(不要求证明);
的单调区间(不要求证明);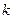 为实常数,解关于
为实常数,解关于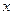 的不等式:
的不等式: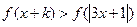
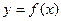
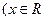 且
且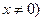 对任意非零实数
对任意非零实数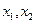 恒有
恒有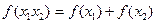 ,且对任意
,且对任意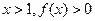 .
. 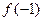 及
及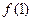 的值;
的值;  的奇偶性;
的奇偶性;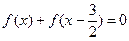 的解.
的解.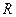 的函数
的函数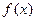 为偶函数,且当
为偶函数,且当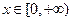 时,
时,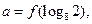
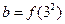 ,
,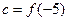 ,则
,则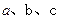 的大小关系是( )
的大小关系是( )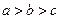
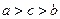
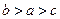
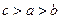
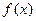 是定义在R上的奇函数,并且当
是定义在R上的奇函数,并且当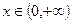 时,
时,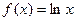 ,那么,
,那么, .
. 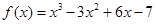 的图象是中心对称图形,其对称中心为
的图象是中心对称图形,其对称中心为